t分布の確率とパーセント点の計算 with Excel
Step 0シチュエーションの設定
ここでは,下のようなt分布表(上側確率)を使って確率あるいはtの値を求める作業を,Excelでの処理に置き換えて見ていきます。
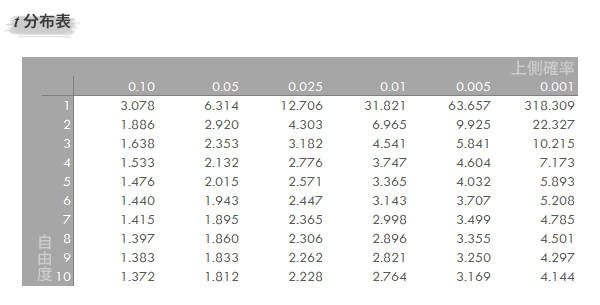
以下共通の設定として,自由度を9と固定して進めます。また0.5を超える片側確率は扱わないものとします。
t から 確率p を求める
Step 1ある t より大きくなる確率上側確率p
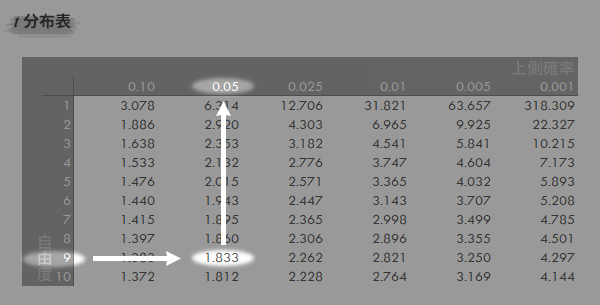
t=1.833のとき,t分布表において上側確率は0.05 (5%)とわかります(下図矢印の参照)。
Step 2T.DIST.RT関数
上側確率は,ExcelではT.DIST.RT関数で求めます。このとき,引数は次のとおりです。
- T.DIST.RT(t, 自由度) ―"Office"
具体的には,下図・下表のような式で上側確率が求められます。
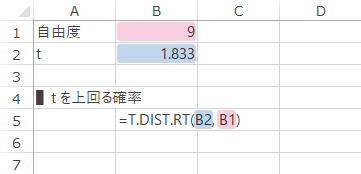
| B5 | =T.DIST.RT(B2, B1) |
|---|
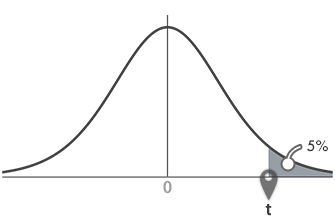
戻り値: 0.050(5%)[※少数点第4位で四捨五入。以下に同じ]。これは,下のグラフ[※イメージ。以下に同じ]のグレーの彩色部分の面積です。
Step 3ある t より小さくなる確率下側確率p
ここでは0より小さなtの値を想定具体的にはt=-1.833とし,このtの場合の下側確率を求めます。
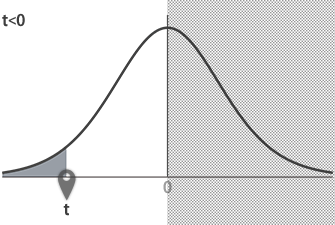
先のt分布表は上側確率のそれゆえにマイナスのtが載っていません。したがってここでのように0より小さなtを扱う場合には,ちょっとばかり戸惑ってしまいます。もっとも,ここで扱うt分布が左右に対称であることを顧みれば,便宜的にtの絶対値をとって鏡面に写したように図を反転させてやると,先のt分布表がそのまま使えることに気づきます。
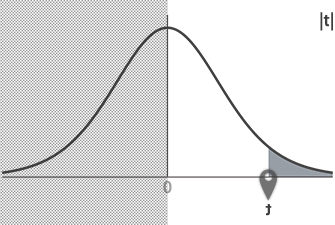
したがって|t|=1.833として先と同様に表から値を読みとると,下側確率は0.05 (5%)とわかります。
Step 4T.DIST.RT, T.DIST関数
ひとつに,Excelでも上の考え方と同様にして,tの絶対値をとって下側確率を求める方法があります。
具体的には,これは下図・下表のような式で求められます。

| B5 | =T.DIST.RT(ABS(B2), B1) |
|---|
また2つ目として,T.DIST関数を用いる方法があります。こちらの場合,先のようにtの絶対値をとる必要はありません(下図)。
- T.DIST(t, 自由度, 関数形式※) ―"Office"
※引数「関数形式」は,[true] の指定で下側(累積)確率が,[false] の指定で確率密度(高さ)が返ります(ここでは後者の指定を必要とするような手続きは登場しません)。
具体的には,下図・下表のような式で下側確率が求められます。
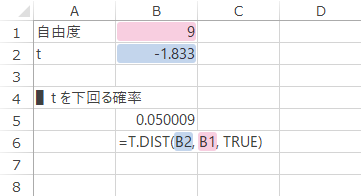
| B6 | =T.DIST(B2, B1, TRUE) |
|---|
戻り値:0.050(5%)。これは,下のグラフのグレーの彩色部分の面積です。
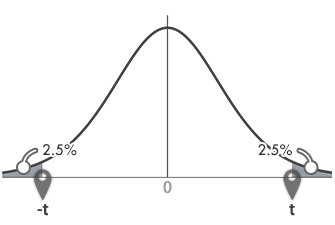
Step 5ある t の絶対値より大きくなる確率両側確率2*p
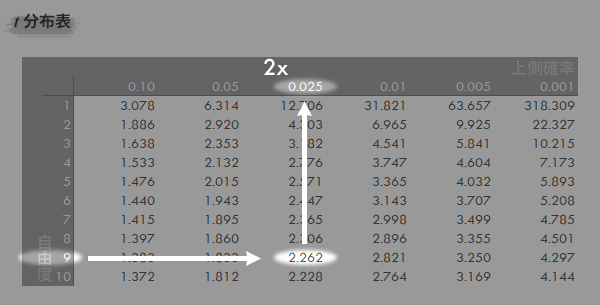
|t|=2.262のとき,t分布表において両側確率は0.05(5%; 上側2つ分2.5%×2)とわかります(下図矢印の参照)。
Step 6T.DIST.2T関数
t分布における両側確率は,T.DIST.2T関数で求めます。このとき,引数は次のとおりです。
- T.DIST.2T(|t|, 自由度) ―"Office"
具体的には,これは下図・下表のような式で求められます。

| B5 | =T.DIST.2T(ABS(B2), B1) |
|---|
戻り値:0.050(5%)。これは,下のグラフのグレーの彩色部分の面積です。
片側確率p(下or上) または 両側確率2*p から t を求める[パーセント点]
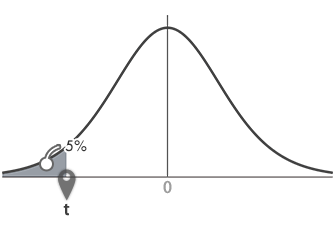
Step 1片側確率p のときの t
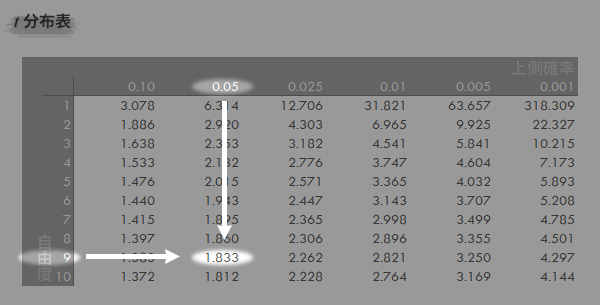
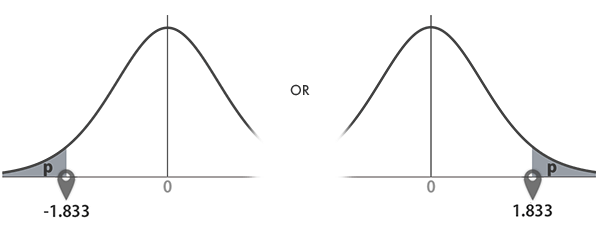
p=0.05のとき,t分布表においてtは1.833とわかります(下図矢印の参照)。2.-Step 3で見たように,pが下側を指して言うなら-1.833とみなします。
Step 2T.INV.2T, T.INV関数
片側(下側or上側)pに対するt(100×pパーセント点)は,T.INV.2T関数で求めます。このとき,引数は次のとおりです。
- T.INV.2T(両側2*p, 自由度) ―"Office"
※最初の引数は「両側2*p」であることに注意を要します。この関数は両側(換算の)確率を要求します。
具体的には,下図・下表のような式でtが求められます。

| B5 | =T.INV.2T(2*B2, B1) |
|---|
戻り値: 1.833。これは,下の右側のグラフの横軸・ポインターが指示する点です。0より大きな方のtのみが返るので,下側確率を念頭に置いた処理の場合,tに負の符号を加えます。
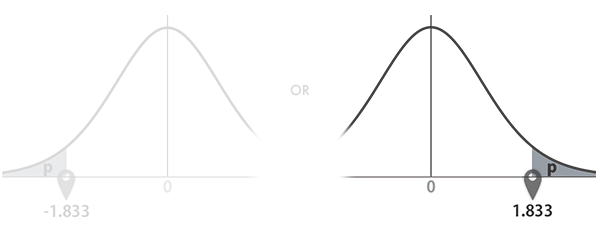
他方,これはT.INV関数を使って求めることも可能です。こちらを選択する場合,tの符号について調整を挟む必要がありません(下図)。
T.INV関数の引数は次のとおりです。
- T.INV(下側p, 自由度) ―"Office"
具体的には,これは下図・下表のような式で求められます。
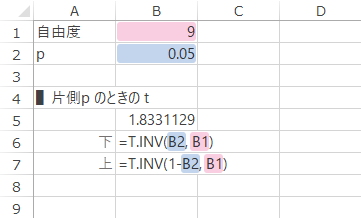
| 下側の場合 | =T.INV(B2, B1) |
|---|---|
| 上側の場合 | =T.INV(1-B2, B1) |
戻り値: -1.833 または 1.833。これは,下のグラフの横軸・各ポインターが指示する点です。
Step 3両側確率2*p のときの t
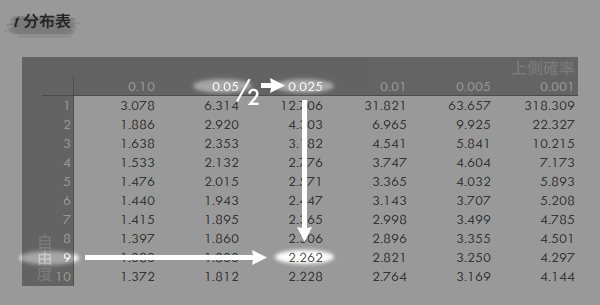
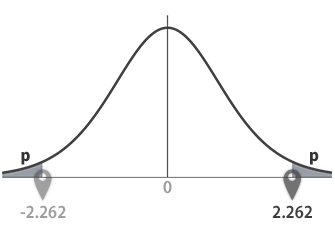
両側確率(2*p)=0.05のとき(片側は両側の半分),t分布表においてtは2.262とわかります(下図矢印の参照)。
Step 4T.INV.2T, T.INV関数
両側2*pに対するパーセント点は,T.INV.2T(version2010以降)関数で求めます。ただし,これにより返ってくるのは0より大きな方のtのみです。この場合の引数は次のとおりです。
- T.INV.2T(両側2*p, 自由度)
具体的に,tは下図・下表のような式で求められます。
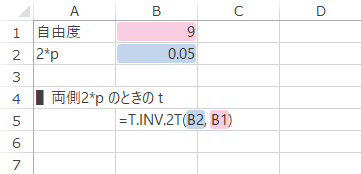
| B5 | =T.INV.2T(B2, B1) |
|---|
戻り値: 2.262。これは,下のグラフの横軸・右側のポインターが指示する点です。
他方,T.INV関数を用いる方法もあります。こちらはいずれかのtを明示的に求めます(下図)。
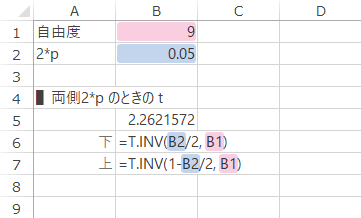
| 0より小さなt | =T.INV(B2/2, B1) |
|---|---|
| 0より大きなt | =T.INV(1-B2/2, B1) |
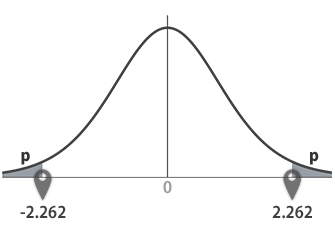
戻り値: -2.262 および 2.262。これは,下のグラフの横軸・両側のポインターが指示する点です。
参考にした書籍
- きたみあきこ(2013)『Excel 関数逆引き辞典パーフェクト 2013/2010/2007/2003対応』翔泳社, pp.666-671.
- 菅 民郎(2013)『Excelで学ぶ統計解析入門 Excel2013/2010対応版』オーム社, pp.171-172.
Next
その他の参照
このサイトの関連How-toです。
- 正規分布の確率とパーセント点の計算
- 標準正規分布の確率とパーセント点の計算
- χ2分布の確率とパーセント点の計算
- F分布の確率とパーセント点の計算
- 母平均の信頼区間の推定
- 分布曲線のグラフ―確率とパーセント点のビジュアライゼーション
メインサイト「ひとりマーケティングのためのデータ分析」の分布に関連するHow-toです。