母分散の信頼区間の推定 with Excel
母分散のχ2推定
Step 0シチュエーションの設定
大学Xのある科目にて500名強の学生にペーパーでの提出を課されたレポートがあります。担当教員は今年度の講義から,学生に対し“2000文字程度”というアバウトな字数指定を「レポートの条件」に加えることにしました。またそれにともない,レポートの最終頁には必ず総字数を明記するよう指示しています。
後日受講者からレポートを回収した際,この教員はここから31名のレポートを無作為に抽出して,この年の学生がどの程度の文字数を狙ってくるのかレポートの最終頁にざっと目を通してみました。具体的に,これは下表のようになりました。
DL
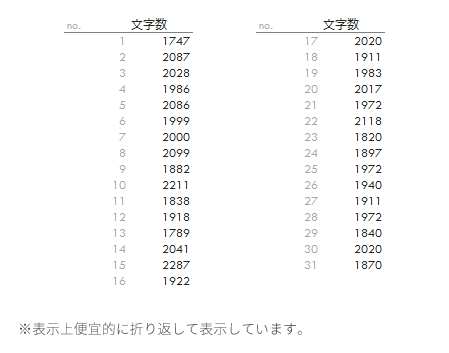
以下,このデータをもとに母分散$σ^2$の区間推定をおこないます。
Step 1前提
母集団は正規分布にしたがうものとします。また母平均$\mu$は未知とします。
Step 2見出しの入力
$σ^2$の信頼区間は次の式によって求められます。
ただし, $n$: 標本サイズ, $s^2$: 不偏分散, $\chi^2(n-1; \alpha/2)$: 自由度$n-1$のときの上側$\alpha/2$パーセント点, $\chi^2(n-1; 1-\alpha/2)$: 自由度$n-1$のときの下側$\alpha/2$パーセント点。
これをシート上で計算するため,下のような見出しを作成しておきます。

Step 3n, df の入力または計算
$n$,自由度を計算または入力します(セルE2, E3)。
なお計算の場合は次式となります。
| n | =COUNT(B2:B32) |
|---|---|
| df | =E2-1 |

Step 4s2の計算
$s^2$を求めます。
式は次のとおりです。
| =VAR.S(B2:B32) |

またここは,step 7の計算式を調整する前提で,不偏分散に代えて偏差平方和を表示させてもOKです。
| Σ(xi-x̄)2 | =DEVSQ(B2:B32) |
|---|
Step 5信頼係数の入力
(仮に)同様の標本抽出から区間推定を繰り返しおこなうことを考えたとき,その繰り返しのなかで一定の幅をもつ区間に母分散$\sigma^2$を捉えられるであろう割合(「信頼係数」)を定めます。一般には0.90・0.95・0.99(百分率での表記の場合,これらを順に“信頼度”90%・95%・99%とも)といったところが利用されます。信頼係数を大きくとれば,区間の幅も広くなります。
ここでは0.95(95%)を選択します。これにより,有意水準(過誤確率)も決まります(1-信頼係数)。
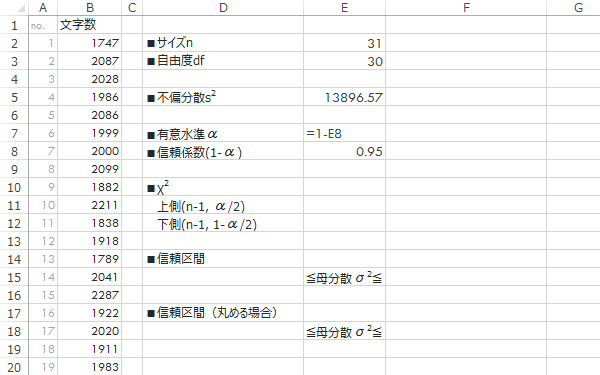
Step 6χ2値の入力または計算
$\chi^2$分布の上下$\alpha/2$パーセント点を計算または入力します(直下は計算の例)。CHISQ.INV.RT関数は上側確率に対する$\chi^2$の値を返すので,下側$\chi^2$はCHISQ.INV.RT($\alpha/2$+信頼係数)で計算します。
| [上側] | =CHISQ.INV.RT(E7/2, E3) |
|---|---|
| [下側] | =CHISQ.INV.RT(E7/2+E8, E3) |
| [上側]互換性関数の場合 | =CHIINV(E7/2, E3) |
|---|---|
| [下側]互換性関数の場合 | =CHIINV(E7/2+E8, E3) |

また直接入力する場合,$\chi^2$分布表から自由度$n-1$のときの上側確率に対応する$\chi^2$値を読み取ります。たとえば先に上げた3つの信頼係数に対応する値を示すと下の表のようになります(自由度30の場合)。
| 90% | 43.773 |
|---|---|
| 95% | 46.979 |
| 99% | 53.672 |
| 90% | 18.493 |
|---|---|
| 95% | 16.791 |
| 99% | 13.787 |
Step 7信頼区間の計算
Step 8信頼区間の計算(桁をくり上げる場合)
任意の桁で丸めるときは,信頼区間を満たすよう,下は切り捨て・上は切り上げで対処します。
| 下側 | =ROUNDDOWN(D15,0) |
|---|---|
| 上側 | =ROUNDUP(F15,0) |

結果: 母分散$\sigma^2$の信頼区間は信頼度95%で8874~24829の間にあると考えられます(標準偏差94~158字)。
参考にした書籍
- 栗原伸一(2011)『入門 統計学 -検定から多変量解析・実験計画法まで-』オーム社, pp.82-85.
- 松原 望・縄田和満・中井検裕(1991)『統計学入門 (基礎統計学)』東京大学教養学部統計学教室編, 東京大学出版会, pp.226-227.
- 上田拓治(2009)『44の例題で学ぶ統計的検定と推定の解き方』オーム社, pp.173-175.
母分散の推定に対応するexcelアドインソフト
- エクセル統計 BellCurve
- 「1標本の推定と検定」「母分散の推定」
- Statcel4(4Stepsエクセル統計)
- 「母数の推定」
その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の有意性検定に関するHow-toです。
