母平均の信頼区間の推定 with Excel
Step 0Case 1 - 4 共通の設定
この頁では推定にあたり,
- 母集団の分散について既知か(:母集団の正規性)
- 標本サイズ$n$が大きいか(:中心極限定理)
について,そのいずれか,あるいは両方を満たす場合に標準正規分布($z$分布)を,そうでなければ$t$分布を利用します。
母分散既知 & 大標本のときのz推定
Case 1-Step 0シチュエーションの設定
家電メーカーY社は比較的需要の安定した商品Aを製造しています。Y社はその商品Aに関して,M県での店頭販売価格を毎年調査しています。
前回は全数調査をおこなっており,今回は標本調査をおこなうことになりました(母標準偏差[母分散]は既知と仮定: 母集団は正規分布に従う)。そこで,M県全域から無作為に選んだAの取扱100店を対象にして,あるとき一斉に価格調査をおこなった結果が下の表です。
以下,このデータをもとにM県における平均店頭販売価格$\mu$の区間推定をおこないます。
DL
Case 1-Step 1前提
- 既知の母分散: 4000000(母標準偏差2000円)
また$n\geqq30$を満たすことから,これを
- 大標本
と判断します(これは一意な基準ではありません[以下Caseに同じ])。
したがってCase 1ではStep 0のいずれの項目も満たすので,
標準正規分布($z$分布)
を利用します。
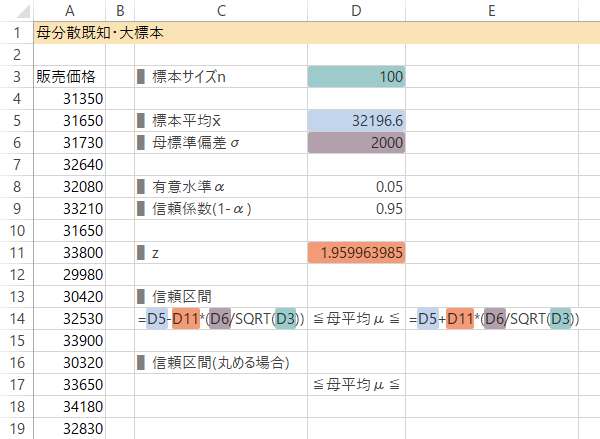
Case 1-Step 2見出しの入力
母平均$\mu$の信頼区間は次の式によって求められます。
ただし, $\bar{x}$: 標本平均, $\sigma$: 母標準偏差, $z(\alpha/2)$: 標準正規分布の上側$\alpha/2$パーセント点。
これをシート上で計算するため,下表のような見出しを作成しておきます。
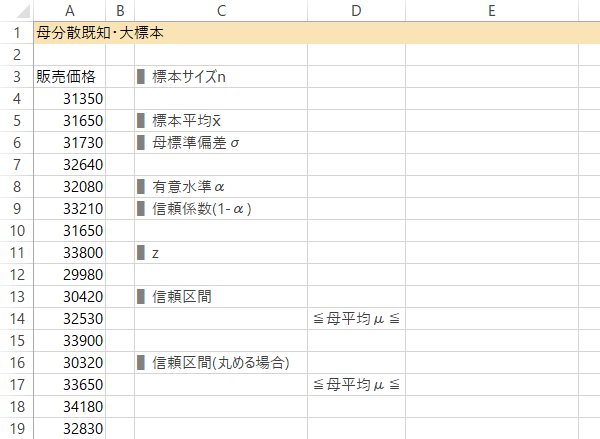
Case 1-Step 3n, x̄, σ の入力または計算
$n$を入力ないし計算します(後者の場合COUNT関数など)。また$\bar{x}$を計算します(AVERAGE関数)。さらに$\sigma$は既知の値を入力します。
![[D5]=AVERAGE(A4:A103)](../../images/confidence-interval/population-mean/case1/step3.png)
Case 1-Step 4信頼係数の決定
(仮に)同様の標本抽出から区間推定を繰り返しおこなうことを考えたとき,その繰り返しのなかで一定の幅をもつ区間に母平均$\mu$を捉えられるであろう割合(「信頼係数」)を定めます。一般には0.90・0.95・0.99(百分率での表記の場合,これらを順に“信頼度”90%・95%・99%とも)といったところが利用されます。信頼係数を大きくとれば,区間の幅も広くなります。
ここでは0.95(95%)を選択します。これにより,有意水準(過誤確率)も決まります(1-信頼係数)。
![[D8]=1-D9](../../images/confidence-interval/population-mean/case1/step4.png)
Case 1-Step 5zの入力または計算
標準正規分布の上側$\alpha/2$パーセント点を計算または入力します(下は計算の例です)。ExcelのNORM.S.INV関数は累積(下側)確率$p$に対する$z$の値を返すので,上側$z$はNORM.S.INV($\alpha/2$+信頼係数)で計算します。つまり,信頼係数を0.95とした場合,$p=0.975$として対応する$z$を求めることになります。
![[D11]=NORM.S.INV(D8/2+D9)](../../images/confidence-interval/population-mean/case1/step5.png)
また直接入力する場合,標準正規分布表から上側$\alpha/2$に対応する$z$を読み取ります。たとえば先に上げた3つの信頼係数に対する上側$z$は,下の表のとおりです。
| 0.90($\alpha/2=0.05$) | 1.64 |
|---|---|
| 0.95($\alpha/2=0.025$) | 1.96 |
| 0.99($\alpha/2=0.005$) | 2.58 |
Case 1-Step 6信頼区間の計算
Case 1-Step 7信頼区間の計算(桁をくり上げる場合)
任意の桁で丸めるときは,信頼区間を満たすよう,下は切り捨て・上は切り上げで対処します。
| 下側 | =ROUNDDOWN(C14, 0) |
|---|---|
| 上側 | =ROUNDUP(E14, 0) |
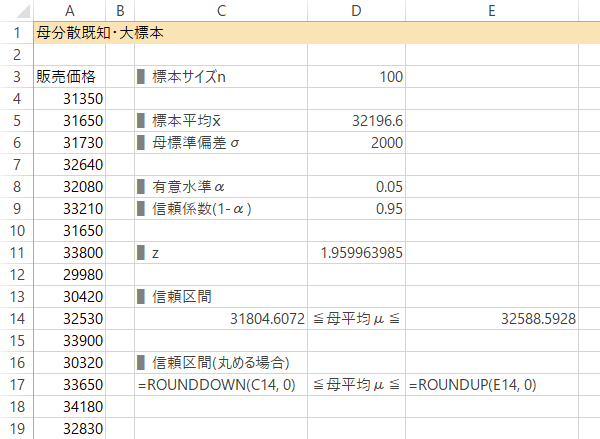
結果: M県での平均店頭販売価格$\mu$は,信頼度95%で31,804~32,589円の間にあると考えられます。
Case 1-Step 8専用の関数を使うなら
上述の経過をブラックボックスにしてもよいのなら,CONFIDENCE.NORM関数によっても同様の計算が可能です。
![[D13]=CONFIDENCE.NORM(D8,D6,D3)](../../images/confidence-interval//population-mean/case1/step8.png)
| 1/2区間 | =CONFIDENCE.NORM(α, σ, n) |
|---|
この場合,戻り値は区間の幅の半分(1/2)です。これを$\bar{x}$に加減して上限・下限を求めます。
母分散既知 & 小標本のときのz推定
Case 2-Step 0シチュエーションの設定
企業調査会社Yのリサーチャー数百人は,1度に1本に限り備品庫よりあたらしい鉛筆を自由に持ち出すことができます。これを持ち出す際には,各自で日付とIDを台帳に残すルールになっています。
あるとき文具を管理する総務部では,ある月の鉛筆の使用本数の平均についてどの程度のものか数字を出す必要に迫られました。過去に全員を対象とした分析をおこなったことはありますが(母標準偏差[母分散]既知と仮定: 母集団は正規分布に従う),あらためて詳細に調べてみるにも時間が十分でないようです。そこで,今回は信頼区間で報告することを決めました。
社員マスタから無作為に28人を抽出し,台帳より使用本数を集計したものが下の表です。このデータから,ある月における鉛筆の平均使用本数$\mu$を推定します。
DL
Case 2-Step 1前提
- 既知の母分散: 2.25(母標準偏差1.5本)
また$n<30$なので,これを
- 小標本
と判断します。
したがってCase 2ではStep 0の片方の項目を満たすので,
標準正規分布($z$分布)
を利用します。
Case 2-Step 2見出しの入力
母平均$\mu$の信頼区間は次の式によって求められます。
ただし, $\bar{x}$: 標本平均, $\sigma$: 母標準偏差, $z(\alpha/2)$: 標準正規分布の上側$\alpha/2$パーセント点。
これをシート上で計算するため,下表のような見出しを作成しておきます。

Case 2-Step 3n, x̄, σ の入力または計算
$n$を入力ないし計算します(後者の場合COUNT関数など)。また$\bar{x}$を計算します(AVERAGE関数)。さらに$\sigma$は既知の値を入力します。
![[D4]=AVERAGE(A4:A31)](../../images/confidence-interval/population-mean/case2/step3.png)
Case 2-Step 4信頼係数の決定
(仮に)同様の標本抽出から区間推定を繰り返しおこなうことを考えたとき,その繰り返しのなかで一定の幅をもつ区間に母平均$\mu$を捉えられるであろう割合(「信頼係数」)を定めます。一般には0.90・0.95・0.99(百分率での表記の場合,これらを順に“信頼度”90%・95%・99%とも)といったところが利用されます。信頼係数を大きくとれば,区間の幅も広くなります。
ここでは0.95(95%)を選択します。これにより,有意水準(過誤確率)も決まります(1-信頼係数)。
![[D8]=1-D9](../../images/confidence-interval/population-mean/case2/step4.png)
Case 2-Step 5zの入力または計算
標準正規分布の上側$\alpha/2$パーセント点を計算または入力します(下は計算の例です)。NORM.S.INV関数は累積(下側)確率$p$に対する$z$の値を返すので,上側$z$はNORM.S.INV($\alpha/2$+信頼係数) で計算します。つまり,信頼係数を0.95とした場合,$p=0.975$として対応する$z$を求めることになります。
![[D11]=NORM.S.INV(D8/2+D9)](../../images/confidence-interval/population-mean/case2/step5.png)
また直接入力する場合,標準正規分布表から上側$\alpha/2$に対応する$z$を読み取ります。たとえば先に上げた3つの信頼係数に対応する$z$は,下の表のとおりです。
| 0.90($\alpha/2=0.05$) | 1.64 |
|---|---|
| 0.95($\alpha/2=0.025$) | 1.96 |
| 0.99($\alpha/2=0.005$) | 2.58 |
Case 2-Step 6信頼区間の計算
Case 2-Step 7信頼区間の計算(桁をくり上げる場合)
任意の桁で丸めるときは,信頼区間を満たすよう 下は切り捨て・上は切り上げで対処します。
| 下側 | =ROUNDDOWN(C14, 1) |
|---|---|
| 上側 | =ROUNDUP(E14, 1) |
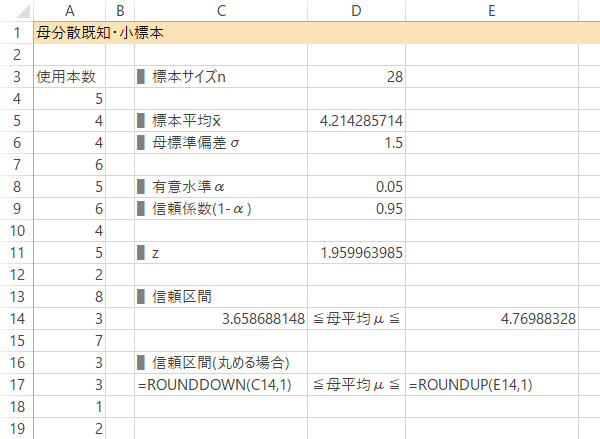
結果: 鉛筆の平均使用本数$\mu$は,信頼度95%で3.6~4.8本の間にあると考えられます。
Case 2-Step 8専用の関数を使うなら
上述の経過をブラックボックスにしてもよいのなら,CONFIDENCE.NORM関数によっても同様の計算が可能です。
![[D13]=CONFIDENCE.NORM(D8,D6,D3)](../../images/confidence-interval/population-mean/case2/step8.png)
| 1/2区間 | =CONFIDENCE.NORM(α, σ, n) |
|---|
この場合,戻り値は区間の幅の半分(1/2)です。これを$\bar{x}$に加減して上限・下限を求めます。
母分散未知 & 大標本のときのz推定
Case 3-Step 0シチュエーションの設定
家電メーカーY社は商品Aを製造しています。Y社はその商品Aに関して,M県での店頭販売価格をはじめて調査することを決めました(母標準偏差[母分散]は未知:母集団の分布は不明)。
もっとも予算の都合,標本調査を実施します。そしてM県全域から無作為に選んだAの取扱100店を対象にして,あるとき一斉に価格調査をおこなった結果が下の表です。
以下,このデータをもとにM県における平均店頭販売価格$\mu$の区間推定をおこないます。
DL
Case 3-Step 1前提
Case 3-Step 2見出しの入力
母平均$\mu$の信頼区間は次の式によって求められます。
ただし, $\bar{x}$: 標本平均, $s$: 標本標準偏差(母分散が未知なので), $z(\alpha/2)$: 標準正規分布の上側$\alpha/2$パーセント点。
これをシート上で計算するため,下表のような見出しを作成しておきます。
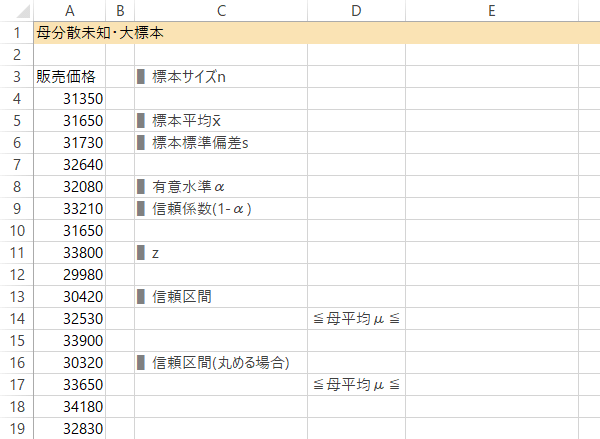
Case 3-Step 3n, x̄, s の入力または計算
$n$を入力ないし計算します(後者の場合COUNT関数など)。また$\bar{x}$を計算します(AVERAGE関数)。さらに$s$を計算します(STDEV.P関数)※。
※$n$のとらえ方によっては不偏標準偏差(このサイトでの用法としては分散の分母が$n-1$の方を指して言います分散・標準偏差と変動係数)を使用した方がbetterな場合もあります(STDEV.S関数)。
![[D5]=AVERAGE(A4:A103), [D6]=STDEV.P(A4:A103)](../../images/confidence-interval/population-mean/case3/step3.png)
Case 3-Step 4信頼係数の決定
(仮に)同様の標本抽出から区間推定を繰り返しおこなうことを考えたとき,その繰り返しのなかで一定の幅をもつ区間に母平均$\mu$を捉えられるであろう割合(「信頼係数」)を定めます。一般には0.90・0.95・0.99(百分率での表記の場合,これらを順に“信頼度”90%・95%・99%とも)といったところが利用されます。信頼係数を大きくとれば,区間の幅も広くなります。
ここでは0.95(95%)を選択します。これにより,有意水準(過誤確率)も決まります(1-信頼係数)。
![[D8]=1-D9](../../images/confidence-interval/population-mean/case3/step4.png)
Case 3-Step 5zの入力または計算
標準正規分布の上側$\alpha/2$パーセント点を計算または入力します(下は計算の例です)。ExcelのNORM.S.INV関数は累積(下側)確率$p$に対する$z$の値を返すので,上側$z$はNORM.S.INV(有意水準$\alpha/2$+信頼係数)で計算します。つまり,信頼係数を0.95とした場合,$p=0.975$として対応する$z$を求めることになります。
![[D11]=NORM.S.INV(D8/2+D9)](../../images/confidence-interval/population-mean/case3/step5.png)
また直接入力する場合,標準正規分布表から上側$\alpha/2$に対応する$z$を読み取ります。たとえば先に上げた3つの信頼係数に対応する上側$z$は,下の表のとおりです。
| 0.90($\alpha/2=0.05$) | 1.64 |
|---|---|
| 0.95($\alpha/2=0.025$) | 1.96 |
| 0.99($\alpha/2=0.005$) | 2.58 |
Case 3-Step 6信頼区間の計算
Case 3-Step 7信頼区間の計算(桁をくり上げる場合)
任意の桁で丸めるときは,信頼区間を満たすよう 下は切り捨て・上は切り上げで対処します。
| 下側 | =ROUNDDOWN(C14, 0) |
|---|---|
| 上側 | =ROUNDUP(E14, 0) |
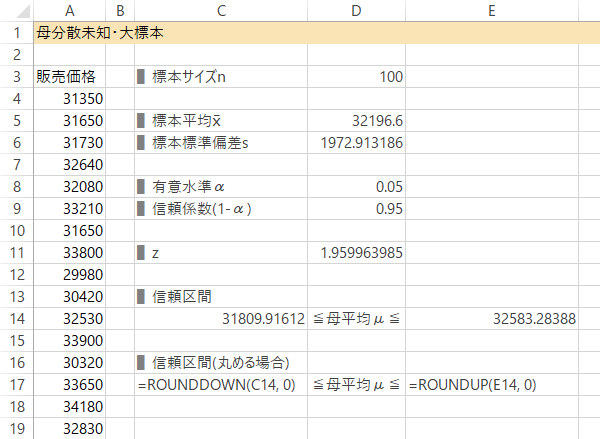
結果: M県での平均店頭販売価格$\mu$は,信頼度95%で31,809~32,584円の間にあると考えられます。
Case 3-Step 8専用の関数を使うなら
上述の経過をブラックボックスにしてもよいのなら,CONFIDENCE.NORM関数によっても同様の計算が可能です。
![[D13]=CONFIDENCE.NORM(D8,D6,D3)](../../images/confidence-interval/population-mean/case3/step8.png)
| 1/2区間 | =CONFIDENCE.NORM(α, s, n) |
|---|
この場合,戻り値は区間の幅の半分(1/2)です。これを$\bar{x}$に加減して上限・下限を求めます。
母分散未知 & 小標本のときのt推定
Case 4-Step 0シチュエーションの設定
企業調査会社Yのリサーチャー数百人は,1度に1本に限り備品庫よりあたらしい鉛筆を自由に持ち出すことができます。これを持ち出す際には,各自で日付とIDを台帳に残すルールになっています。
あるとき文具を管理する総務部では,ある月の鉛筆の使用本数の平均について,どの程度のものか数字を出す必要に迫られました。過去にこうした分析をおこなったことはなく,あらためての全数調査も繁忙により難しい状況にあります(母標準偏差[母分散]未知:母集団の分布は不明)。そこで,今回は標本調査により信頼区間で報告することを決めました。
社員マスタから無作為に28人を抽出し,台帳より使用本数を集計したものが下の表です。このデータから,ある月における鉛筆の平均使用本数$\mu$を推定します。
DL
Case 4-Step 1前提
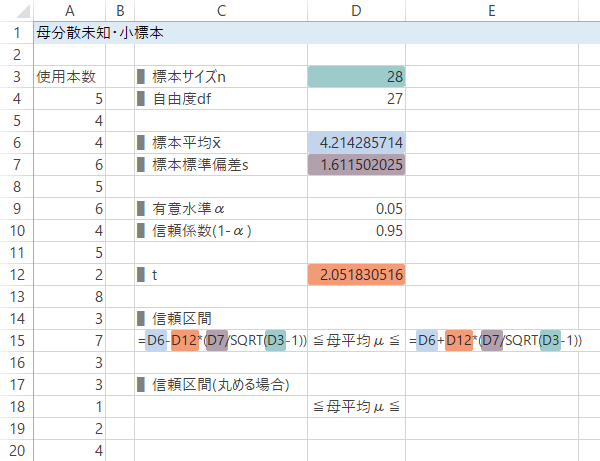
Case 4-Step 2見出しの入力
信頼区間は次の式によって求めます。
ただし, $\bar{x}$: 標本平均, $s$: 標本標準偏差(母分散が未知なので), $t(n-1; \alpha/2)$: 自由度$n-1$の$t$分布の上側$\alpha/2$パーセント点。
これをシート上で計算するため,下表のような見出しを作成しておきます。
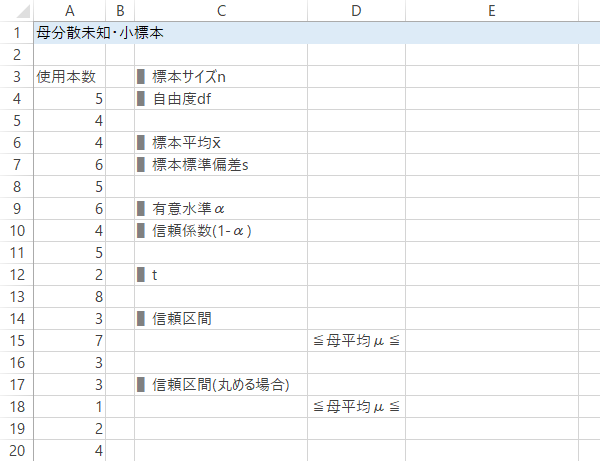
Case 4-Step 3n, df, x̄, s の入力または計算
$n$,自由度を入力ないし計算します(計算の場合COUNT関数など)。また$\bar{x}$を計算します(AVERAGE関数)。さらに$s$を計算します(STDEV.P関数)。
![[D6]=AVERAGE(A4:A31), [D7]=STDEV.P(A4:A31)](../../images/confidence-interval/population-mean/case4/step3.png)
Case 4-Step 4信頼係数の決定
(仮に)同様の標本抽出から区間推定を繰り返しおこなうことを考えたとき,その繰り返しのなかで一定の幅をもつ区間に母平均$\mu$を捉えられるであろう割合(「信頼係数」)を定めます。一般には0.90・0.95・0.99(百分率での表記の場合,これらを順に“信頼度”90%・95%・99%とも)といったところが利用されます。信頼係数を大きくとれば,区間の幅も広くなります。
ここでは0.95(95%)を選択します。これにより,有意水準(過誤確率)も決まります(1-信頼係数)。
![[D9]=1-D10](../../images/confidence-interval/population-mean/case4/step4.png)
Case 4-Step 5tの入力または計算
自由度$n-1$の$t$分布の上側$\alpha/2$パーセント点を計算または入力します(下は計算の例です)。ExcelのT.INV.2T関数は自由度$n-1$のときの両側確率$p$(NORM.S.INVとの違い)に対する上側の$t$の値を返すので,T.INV.2T($\alpha$, 自由度)として計算します。つまり,信頼係数を0.95とした場合,$p=0.05$として対応する$t$を求めることになります。
![[D12]=T.INV.2T(D9,D4)](../../images/confidence-interval/population-mean/case4/step5.png)
また直接入力する場合,$t$分布表から自由度$n-1$のときの上側$p$に対応する$t$を読み取ります。たとえば先に上げた3つの信頼係数に対応する上側$t$(自由度27のとき)は,下の表のとおりです。
| 0.90($\alpha/2=0.05$) | 1.703 |
|---|---|
| 0.95($\alpha/2=0.025$) | 2.052 |
| 0.99($\alpha/2=0.005$) | 2.771 |
Case 4-Step 6信頼区間の計算
Case 4-Step 7信頼区間の計算(桁をくり上げる場合)
任意の桁で丸めるときは,信頼区間を満たすよう 下は切り捨て・上は切り上げで対処します。
| 下側 | =ROUNDDOWN(C15, 1) |
|---|---|
| 上側 | =ROUNDUP(E15, 1) |
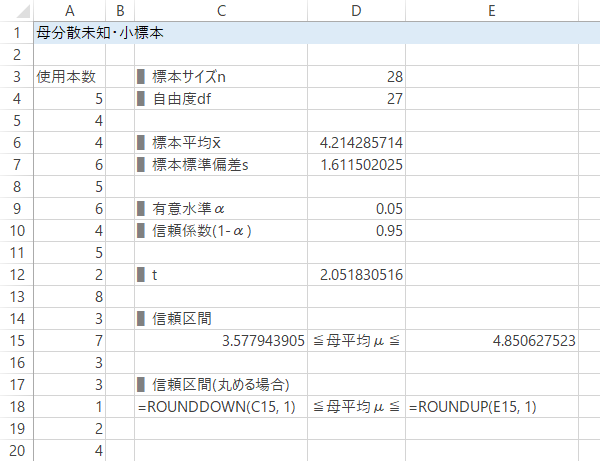
結果: 鉛筆の平均使用本数$\mu$は,信頼度95%で3.5~4.9本の間にあると考えられます。
Case 4-Step 8専用の関数を使うなら
上述の経過をブラックボックスにしてもよいのなら,CONFIDENCE.T関数によっても同様の計算が可能です。この場合,不偏標準偏差(このサイトでの用法としては分散の分母が$n-1$の方;STDEV.S関数の戻り値分散・標準偏差と変動係数)に差し替えて計算します。
![[D7]=STDEV.S(A4:A31), [D14]=CONFIDENCE.T(D9,D7,D3)](../../images/confidence-interval//population-mean/case4/step8.png)
| 1/2区間 | =CONFIDENCE.T(α, 不偏標準偏差, n) |
|---|
この場合,戻り値は区間の幅の半分(1/2)です。これを$\bar{x}$に加減して上限・下限を求めます。
参考にした書籍
- 栗原伸一(2011)『入門 統計学 -検定から多変量解析・実験計画法まで-』オーム社, pp.58-72.
- アミール D. アクゼル・ジャヤベル ソウンデルパンディアン(2007)『ビジネス統計学[上]』鈴木一功監訳, 手嶋宣之・原 郁・原田喜美枝訳, ダイヤモンド社, pp.270-289.
- 石村光資郎(2012)『身近な事例で学ぶやさしい統計学』オーム社, pp.101-113.
- 上田拓治(2009)『44の例題で学ぶ統計的検定と推定の解き方』オーム社, pp.154-157.
母平均の推定に対応するExcelアドインソフト
- エクセル統計 BellCurve
- 「1標本の推定と検定」「母平均の推定」(z推定・t推定|有限母集団修正も可能)
- Statcel4(4Stepsエクセル統計)
- 「母数の推定」
その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の有意性検定に関するHow-toです。