基本統計量の計算 with Excel 3/3
分散・標準偏差と変動係数の計算
Step 0シチュエーションの設定
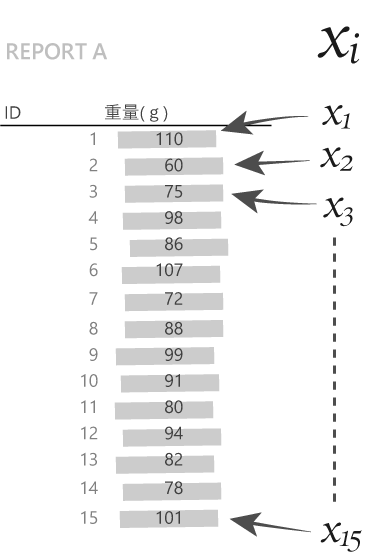
下表は,マーケティング調査会社Xが,ある1日に顧客に郵送した2種類のレポート(A・B)の重量です。送付の前にそれぞれ数百あるレポートの中から無作為に15のアイテムを抽出し,それを記録したものです。
DL
このデータから,両者の分散・標準偏差と変動係数を求めます。
なお 以下文中※印注の用語については,一意的に使用されているものではありません(cf.「名称の混乱」標準偏差 ―"Wikipedia")。このサイトでは,これら用語の字句としての適否は無視し,分母を区別する“記号”としてのみ扱います。たとえば,ここにいう「不偏標準偏差」は字句の指すところとは性格を異にします。これに抵抗があれば,たとえば「不偏分散の正の平方根の 標準偏差」などに適宜読みかえてください。
ざっくりとした言い方をすれば,「分散」や「標準偏差」の指すものが人によって思いがけず異なり齟齬をきたすことがあるので,レポートや分析資料などで第三者の目を意識する必要のある場合,アルファベット・ギリシャ文字による表記の方法も含め,数式による定義を入れておいた方がbetterだとは思います。
分散(Variance)
[ギリシャ文字・アルファベットであらわされるとき]
- たとえば,
- 母分散: σ2
- 分散: s2
- 分母の違いで区別するなら,
- nの分散: s2
- n-1の分散: u2
- など。
Step 1分散の計算|Var.P, Var.S関数
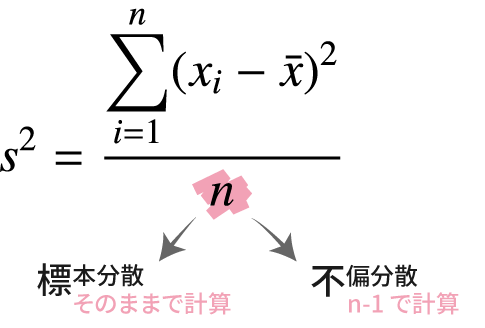
Excelでは,分散は関数で求めることができます。この場合,偏差平方和を
- サンプルサイズnで割るか(標本分散※: 標本の分散)
- n-1で割るか(不偏分散※: 母分散の推定量)
によって関数を使い分けます。下表はその一覧です。
| 標本分散 | 不偏分散 |
|---|---|
| Var.P | Var.S |
これらの関数を利用してレポートA・Bの分散をともに求めるとき,具体的には式を下図のとおり組み立てます(例示のため標本・不偏ともに求めます)。
なお,Var.P,Var.Sの両関数は,Excel 2010から組み込まれた関数です。以降のバージョンでもこれらの旧関数であるVarP,Varという名称の関数が残置され使用可能になっていますが,とりわけ"Officeサポート"サイトにて,
新関数の方がより精度が高く旧関数は
将来のバージョンでは利用できなくなる可能性がある
ことが強調されていることに鑑みると,特段の事情でもない限り第一の選択とはしないほうがよさそうです。
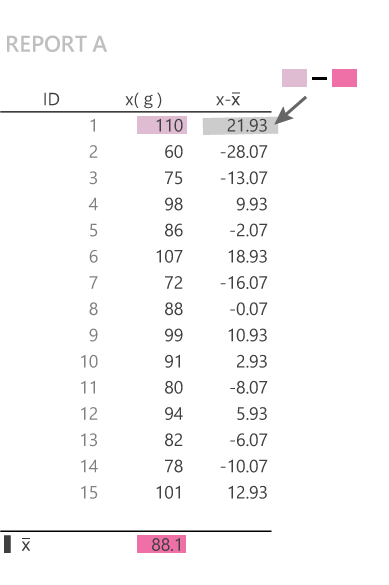
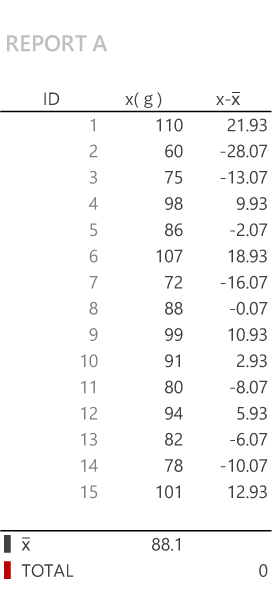
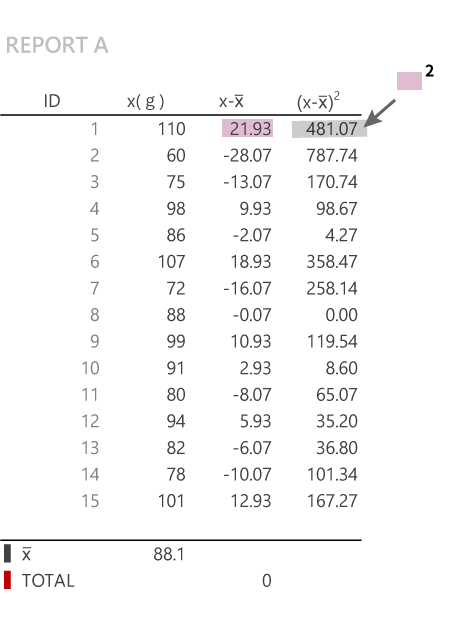
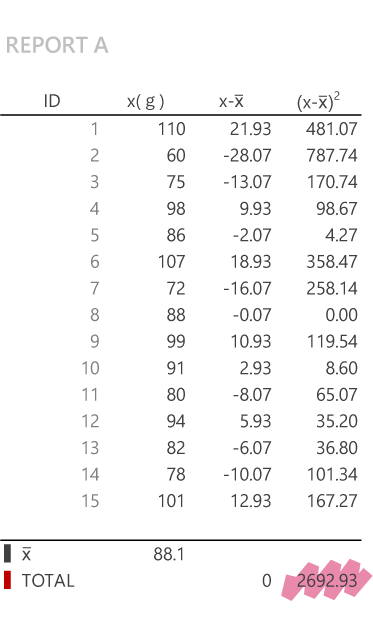
Var系関数に拠らず定義式に沿って計算する場合(デフォルトで非表示|クリックで展開)
Step 2分散・計算完了
レポートA・Bの分散は,次のとおりです。
標準偏差(Standard Deviation, SD)
[ギリシャ文字・アルファベットであらわされるとき]
- たとえば,
- 母標準偏差: σ
- 標準偏差: s
- 分母の違いで区別するなら,
- nの標準偏差: s
- n-1の標準偏差: u
- など。
Step 3標準偏差の計算|StDev.P, StDev.S関数
つづいて標準偏差を求めます。こちらも関数で求めることができます。この場合も同様に,
- 標本分散の√をとるか(標本標準偏差※: 標本の標準偏差)
- 不偏分散の√をとるか(不偏標準偏差※)
によって関数を使い分けます。下表はその一覧です。
| 標本標準偏差 | 不偏標準偏差 |
|---|---|
| StDev.P | StDev.S |
これらの関数を利用してレポートA・Bの分散をともに求めるとき,具体的には式を下図のとおり組み立てます(例示のため標本・不偏ともに求めます)。
なお,こちらのStDev.P,StDev.Sの両関数も,Excel 2010から組み込まれた関数です。同じように以降のバージョンでもこれらの旧関数であるStDevP,StDevという名称の関数が残置され使用可能になっていますが,とりわけ"Officeサポート"サイトにて,
新関数の方がより精度が高く旧関数は
将来のバージョンでは利用できなくなる可能性がある
ことが強調されていることを鑑みれば,やはり特段の事情でもない限り第一の選択とはしないほうがよいかと思います。
StDev系関数に拠らず定義式に沿って計算する場合(デフォルトで非表示|クリックで展開)
Step 4標準偏差・計算完了
レポートA・Bの標準偏差は,次のとおりです。
変動係数(Coefficient of Variation, CV)
Step 5変動係数の計算|標準偏差÷平均
たとえば不偏標準偏差に関して,レポートAとBとでは大きな差があります(上表。13.9gと39.7g)。そのまま単純な比較をすれば,Bの方がバラツキが大きいことは明白です。ただし,平均の違いに明らかなように,レポートAとBは同性質の商品ではありません。分布が異なる以上,そのまま単純に比較をしても腑に落ちないところがあります。
こうした場合,元データが比尺度であれば,変動係数で(平均の大きさをモノサシ[=いくつ分か]にして)相対的に比べることができます。
変動係数(単位なし) = 標準偏差 / 算術平均
Excelの上では,これは下表のように求められます。ただし例示のため,(1)標本標準偏差,(2)不偏標準偏差 の両者をもとにした,いずれの結果とも示します。
Step 6異なる商品のバラツキを比較する
レポートA・Bの変動係数は,次のとおりです。
たとえば不偏標準偏差から計算した変動係数の場合,下のように
- レポートA(平均の15.7%)>レポートB(平均の8.1%)
となりました。よって両者の変動係数での比較では,Bの方が小さいことがわかります。
ただし計算式にて自明なように,分母に算術平均をとる以上,これが0や負の値をとるような性質の対象に変動係数を利用するのは馴染まないことを含みおく必要があります。
これらの統計量が計算できるExcelアドインソフト
- エクセル統計 BellCurve
- 「基本統計・相関」「記述統計量」計算の設定項目
- Statcel4(4Stepsエクセル統計)
- 「基本統計量」
その他の参照
メインサイト「ひとりマーケティングのためのデータ分析」の基本統計に関連するHow-toです。

![[B23]=VAR.P(B4:B18),[B24]=VAR.S(B4:B18),[F23]=VAR.P(F4:F18),[F24]=VAR.S(F4:F18)](../../images/fundamental-statistics/page3/step1.svg)
![TeX: \[ s^{2} = \frac{ \displaystyle \sum_{i=1}^n (x_{i} - \bar{x})^{2} }{ \displaystyle n } \]](../../images/fundamental-statistics/page3/fm-variance.svg)


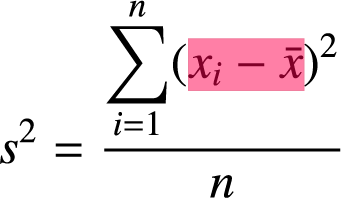

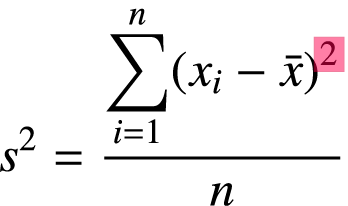
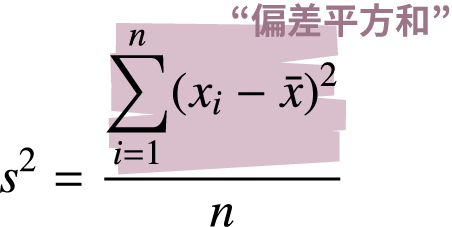

![[B23]=D21/A18, [B24]=D24/(A18-1)](../../images/fundamental-statistics/page3/variance-sub14@1x.png)

![[B27]=STDEV.P(B4:B18),[B28]=STDEV.S(B4:B18),[F27]=STDEV.P(F4:F18),[F28]=STDEV.S(F4:F18)](../../images/fundamental-statistics/page3/step3.svg)
![TeX: \[ s = \sqrt{ \frac{ \displaystyle \sum_{i=1}^n (x_{i} - \bar{x})^{2} }{ \displaystyle n } } \]](../../images/fundamental-statistics/page3/fm-stdev.svg)

![[B26]=SQRT(B23),[B27]=SQRT(B24)](../../images/fundamental-statistics/page3/standarddeviation-sub2@1x.png)

![[B31]=B27/B20,[B32]=B28/B20,[F31]=F27/F20,[F32]=F28/F20](../../images/fundamental-statistics/page3/step5.svg)
