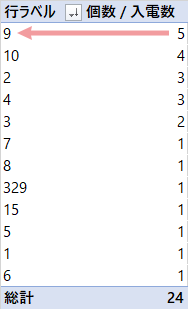基本統計量の計算 with Excel 2/3
中央値・最頻値の計算
中央値[メディアン, 中位数](Median)
Step 0シチュエーションの設定
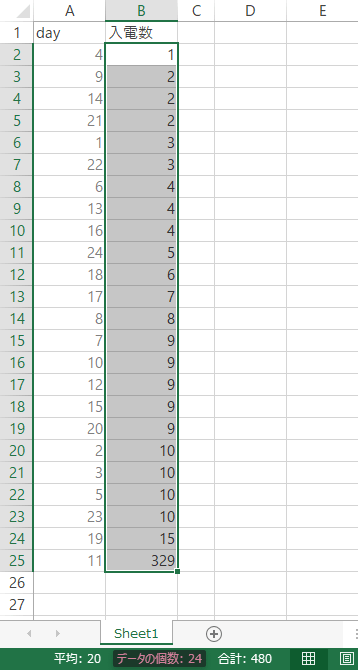
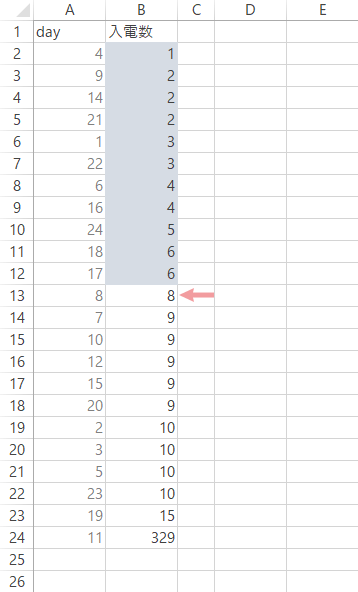
下表は,ネット通販X社のある月の営業日(計24日)に入ったクレーム受信件数(「入電数」)の記録です。
第11営業日には,交通事情に伴う商品の遅配が発生し,ふだんより大幅に件数が増加しました。
DL
この月の受信の平均を求めると,下図のとおり20という値が出てきます。
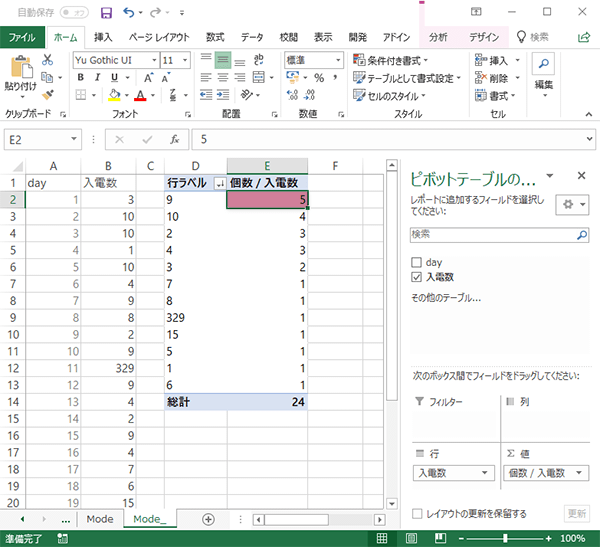
さて,受信件数の平均“20”は,実際に記録された24日分のデータにおいて,23日分の記録を上回る値であることが認められます。このように,ほぼすべてのデータを凌駕するような値を「代表値」として用いるのは,さすがにどこか躊躇を覚えないでもありません。そこで受信件数をあらためてカウントし,グラフ化すれば
なるほどこの“20”の背景には,極端な外れ値の強い影響力が察せられるところです。参考までに,極端な外れ値つまり11日目のクレームを異常値として除外すれば,平均は6.6まで下がります。
ただ,今後におよぶ営業環境に考えを巡らすと,他方でこうした極端な値を安直に外してしまっていいものか,Xは判断を悩んだのも事実です。そこでXは思慮を重ねた結果,
- 分布がキレイである保証は今後ともどこにもない(さらにゆがむかもしれない)
- 可能であれば,記録にきちんと登場する値の方が実感がわきやすい(たとえば先の20や6.6といった値は,実際の記録には存在しないという意味では現実感に欠ける見方もある)
といった点で,結論としては代表値として平均を使用しないことを決めました。
他の代表値としては,中央値や最頻値といったものが利用できます。以下順に,これらを求めるための手続きです(関数を使用しない場合のアプローチについても併記していきます)。
Step 1中央値の計算/Median関数
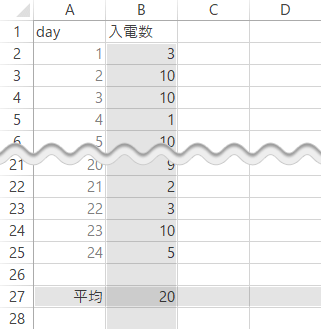
中央値は,ExcelではMedian関数により求められます。
![[E2]=median(b2:b25)](../../images/fundamental-statistics/page2/median1.png)
Median関数に拠らず求める場合(デフォルトで非表示|クリックで展開)
Step 2中央値・計算完了
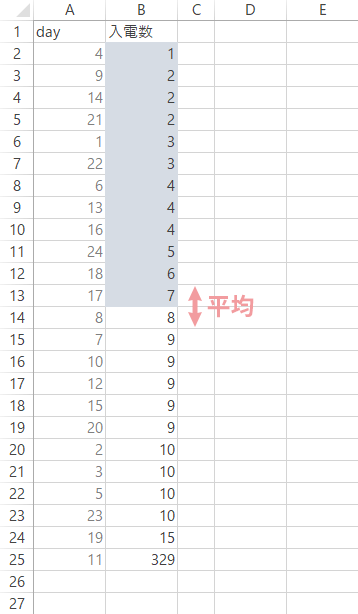
この月の受信件数の中央値は,7.5と求められました。
最頻値[モード](Mode)
Step 3最頻値の計算/Mode.Sngl関数
つづいて最頻値を計算します。Excelでは,最頻値の計算にMode.Sngl関数が使用できます。なおこの関数にいう「最頻値」は連続量を対象としたものでなく,離散量を対象としたものです(cf. 最頻値 ―"日経リサーチ")。
![[E4]=mode.sngl(b2:b25)](../../images/fundamental-statistics/page2/mode1.png)
Mode関数に拠らず求める場合(デフォルトで非表示|クリックで展開)
Step 4最頻値・計算完了
受信件数の最頻値は,9であることがわかりました。
Step 5付記(1)
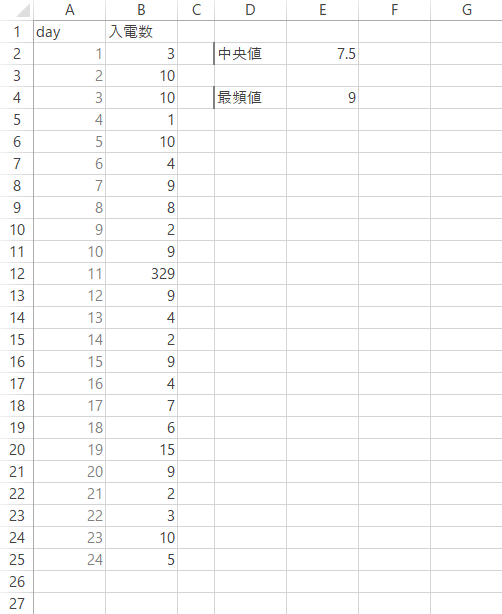
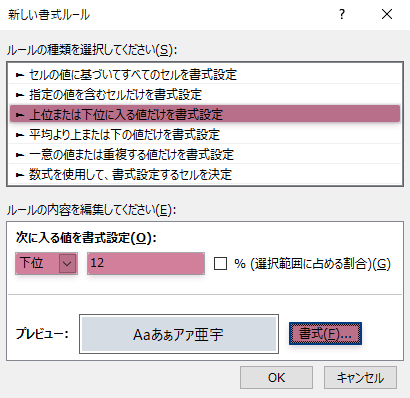
もっとも,最頻値はひとつだけしか出現しないというわけでもありません。多峰型の分布のもとでは,結果としていくらかの最頻値を観測することがあります。これをそのまま代表値として用いるのが相応しいかはまた別の注意が必要かとは思いますが,ここでは参考までに,あらたに下のような単純なデータを用意して,9・10の2つの最頻値を導き出せる場合の処理について加えておきたいと思います。
このとき,Mode.Sngl関数は最初にカウントできた最頻値(ここでは9のほう)のみ返すといった点は含みおく必要があります。つまり,その他にも出現するかどうかについては,無関心です(それが悪いというわけでなく,分布の単峰性が自明な場合などに向く軽快な関数であるという話です)。
DL
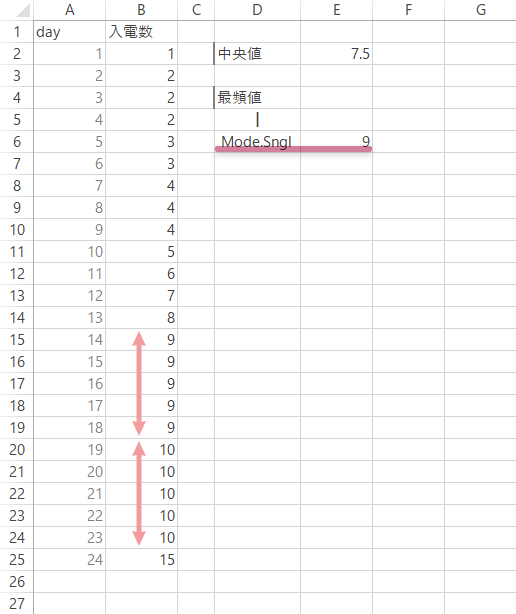
Step 6付記(2)
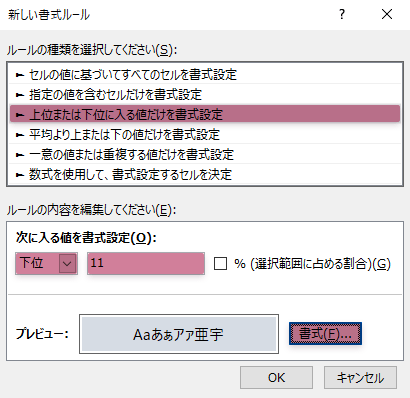
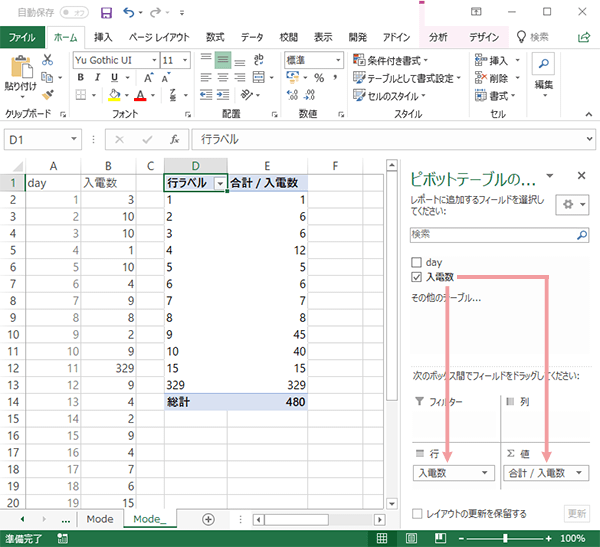
このように2つ以上の最頻値が予見されるような場合の処理としては,Mode.Mult関数が利用できます(配列数式)。
この場合,まずは予見される数にざっくりと目途をつけ,それにいくらかの余裕を加えた数だけセル範囲を選択します(ぶっちゃけ,“テキトー”な数の選択でかまいません。ここで選択した領域に結果が返ります)。
![[e8]=mode.mult(b2:b25)](../../images/fundamental-statistics/page2/mode4.png)
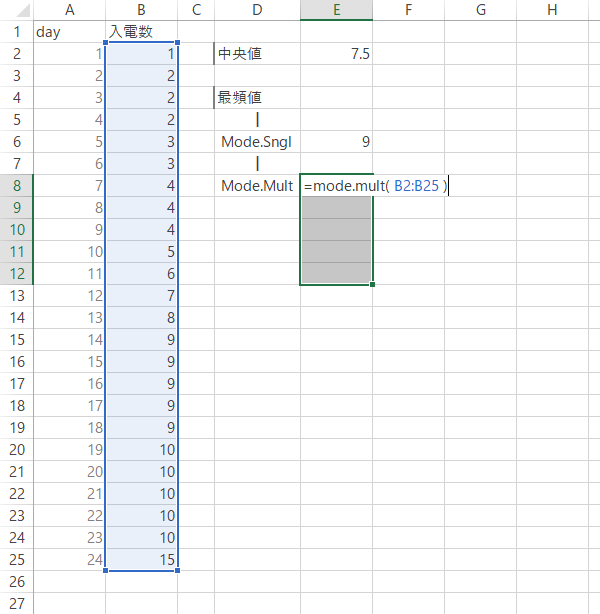
Step 7付記(3)
そして選択を維持したまま,Mode.Mult関数で数式を作成し,[Ctrl]+[Shift]+[Enter]キーで数式を確定します。
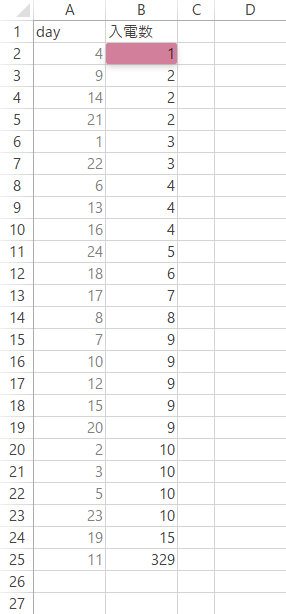
Step 8付記(4)
これにより,下の図のように複数の値が正しく返ります(強調部分の,最初の2つの数字)。
なお「#N/A」は“該当なし”すなわち最初に#N/Aが表示されたセルまでの値をもって,すべての値が返されたことを意味します。
![[e8-e12] 9, 10, #N/A, #N/A, #N/A](../../images/fundamental-statistics/page2/mode6.png)
Next
その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の基本統計に関連するHow-toです。


![[グループの基準]入電数, [集計の方法]データの個数, [集計するフィールド]入電数, [チェック]現在の小計をすべて置き換える・集計行をデータの下に挿入する](../../images/fundamental-statistics/page2/mode-sub3.png)