基本統計量の計算 with Excel 1/3
算術平均・幾何平均・加重平均の計算
算術平均[相加平均, 単純平均](Mean)
Step 0シチュエーションの設定
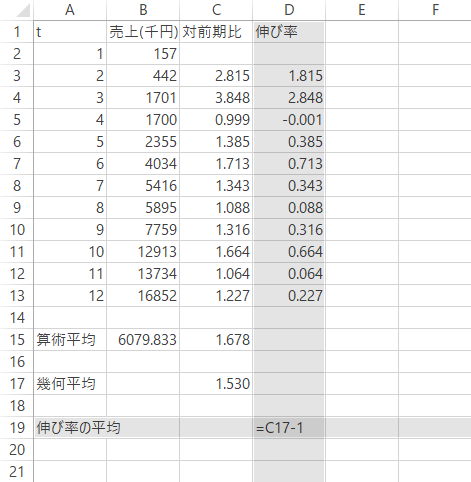
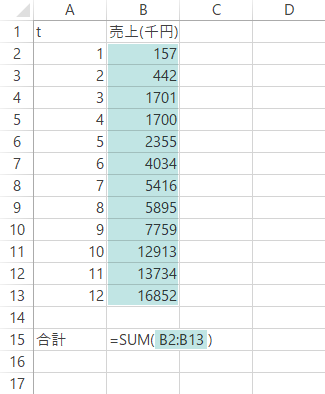
下表は,企業Xの事業Yに関する12期(t)の売上です。
DL
Step 1AVERAGE関数
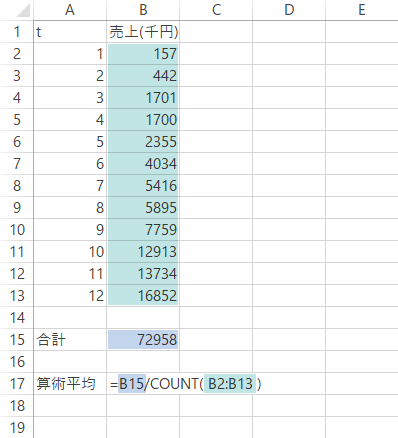
算術平均は,ひろく「平均」と呼ばれるところの値です。これはExcelではAverage関数により求められます。
![[B15]=average(b2:b13)](../../images/fundamental-statistics/page1/mean-2.png)
Average関数に拠らず定義式に沿って計算する場合(デフォルトで非表示|クリックで展開)
Step 2算術平均・計算完了
12期の売上の算術平均は,次のとおりです。
幾何平均[相乗平均](Geometric Mean)
Step 0シチュエーションの設定
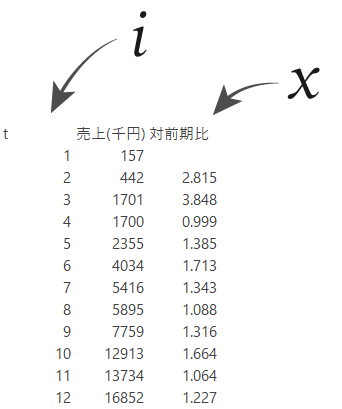
ここで先の表(企業Xの事業Yに関する12期の売上)に関して,対前期比を加えてみます(下図)。
![[C列]対前期比を追加](../../images/fundamental-statistics/page1/geomean1-1.png)
この対前期比について,算術平均を計算するとどういった値が導かれるのかとりあえず安直に11期の平均を求めてみると,1.678(倍)といった値が出てきました。
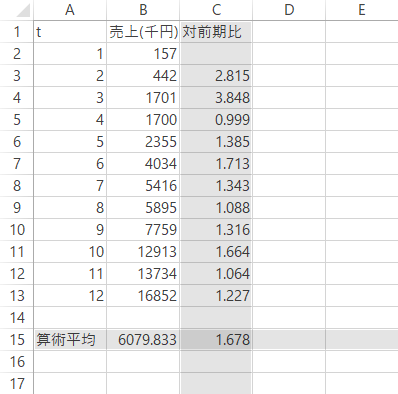
はたしてこの値が,対前期比の“平均”をあらわすものとして妥当なのかどうか,確認をしてみたいと思います。
具体的には1期目の売上を所与として,期を経るごとに1.678倍していきます。そして12期目にどのような値が出現するのかを見ていくと
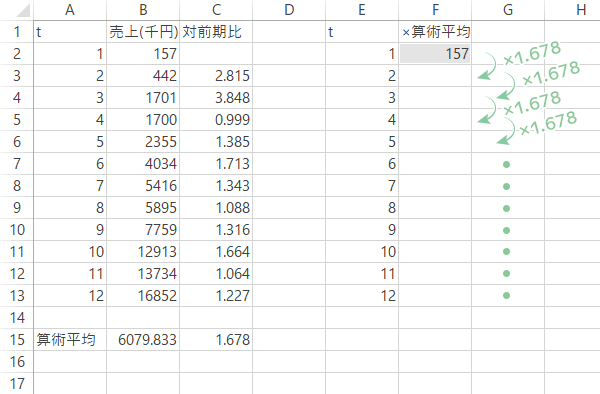
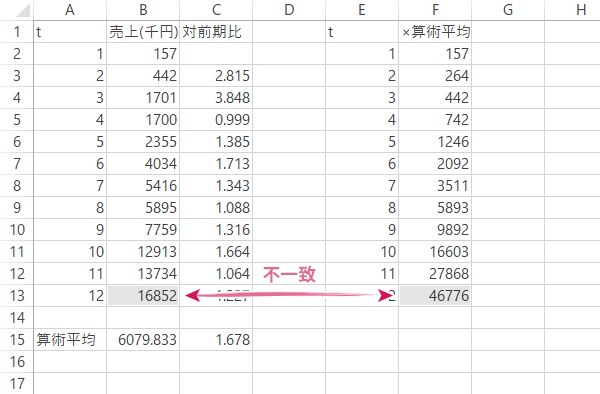
下のように,実際の12期目の売上(16852千円)よりはるかに大きな値が出てきました。
このように,比の平均をとる場合には,算術平均では的を射ないところがでてきます。そこで,これを幾何平均に替えてみたいと思います。
Step 1GEOMEAN関数
幾何平均は,ExcelではGeomean関数により求められます。
![[c17]=geomean(c3:c13)](../../images/fundamental-statistics/page1/geomean2.png)
GeoMean関数に拠らず定義式に沿って計算する場合(デフォルトで非表示|クリックで展開)
Step 2幾何平均・計算完了
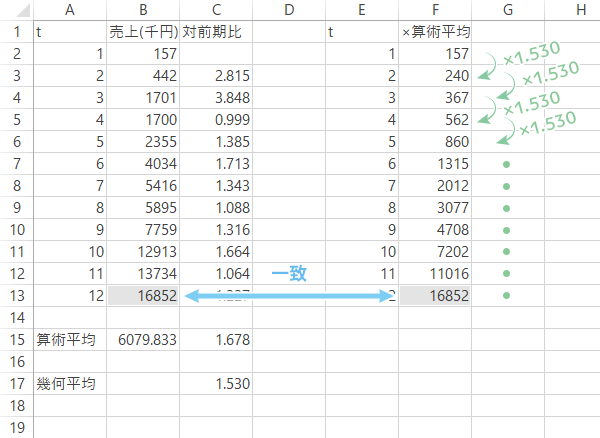
対前期比の幾何平均は,1.530と求められました。
Step 3付記:確認
リードの部分(「シチュエーションの設定」)と同様にして,はたしてこの値で妥当なのかどうかを確認しておきたいと思います。
1期目の値を所与として,先と同様に,期を経るごとに1.530倍していくと12期目で出てきた値は売上のそれと等しくなっていることがわかります。したがって,「対前期比」のように“前期のx倍”に関して平均を求めるような場合,算術平均よりも幾何平均を用いた方がハマりがよいです。
ただし,幾何平均の計算では0および負の値をあつかうことができません(cf. 幾何平均 ―"Wikipedia")。
したがって「対前期比」でなく,当期と前期の差に注目する「伸び率」などに関しては,往々にして上記の性質に触れてしまいます。これに平均を据えておきたいとき,伸び率x%+1=対前期比となる点に鑑みて,「対前期比」の幾何平均から1を引いた値を便宜的にあてておくのもひとつの方法かと思います。
「2.幾何平均」に関して参考にしたWebサイト
- 船津好明(-)「個別データの幾何平均」(2014.6.閲覧)
- 熊本国府高等学校PC同好会(2009u)「率(割合)に注意! … 同率の利益と損失,収支は?」(2014.6.閲覧)
加重平均(Weighted Mean)
Step 0シチュエーションの設定
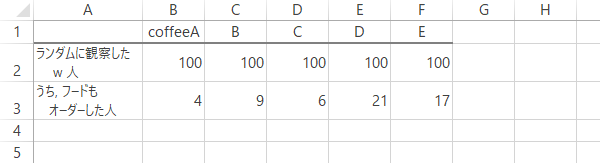
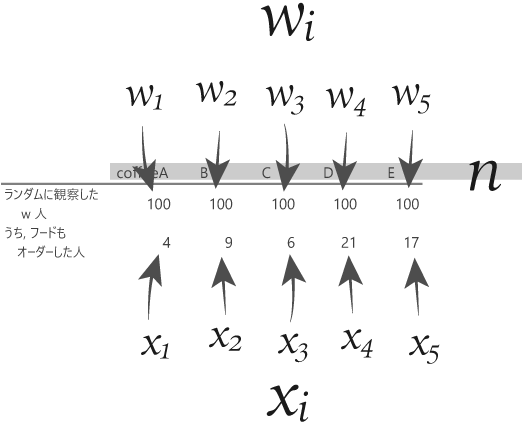
コーヒーチェーンXは,いくらか前にライバルチェーンYの調査をおこないました。そのひとつに,Yが販売するコーヒー品目A~Eをオーダーする顧客の行動を調べたものがあります。
とりわけ,ここではそのうち次のデータに注目したいと思います。
“品目の別に100人ずつ均等にオーダーを観測したところ,
同時にフードメニューもオーダーしたのはA~Eの順に4, 9, 6, 21, 17人であった”
以下のとおり,これを表にしてみます。
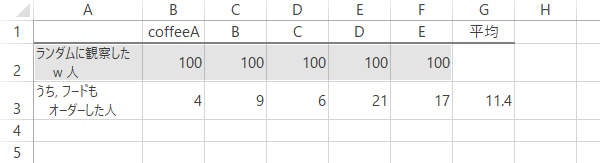
100人ずつ観測した結果としてフードメニューを同時にオーダーした人の平均を求めるとなれば,
感覚的には,下のような計算をまずは想起するところでしょうか。
![[g3]=AVERAGE(B3:F3)](../../images/fundamental-statistics/page1/weightedmean1-4.png)
これによると,平均は11.4人となります。
![[g3]11.4](../../images/fundamental-statistics/page1/weightedmean1-5.png)
?
はたして,この“平均”は的を射たものなのか,どこか不安をおぼえます。この不安の正体は,おそらく下図網掛け部を無視したところにありそうな気がします。
以下では,これを無視しないで再処理してみたいと思います(加重平均)。
Step 1定義式
加重平均は,次の式で求めます。
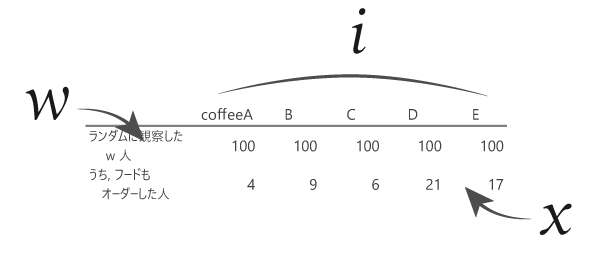
Step 2記号の意味(1)
先のシート構成のとき,式の中の記号i,x,wは順にコーヒー品目「A~E」の序列,「うち,フードもオーダーした人」,「ランダムに観測したw人」の行に充てることができます。
ここでは特に,以下wのことをウエイトと,xのことを観測値と呼んでいきたいと思います。
Step 3記号の意味(2)
すなわちxiは,観測値のi番目の要素のことを,wiは,i番目のウエイトを意味します。またnはコーヒー品目の数(=Xiないしはwi要素の数)となります。
Step 4定義式の分子・「ウエイト×観測値」の総和の計算(1)
最初に,式の分子の部分(赤い囲み)から計算したいと思います。これはウエイト×観測値の総和です。
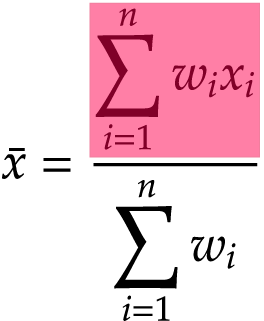
Step 5定義式の分子・「ウエイト×観測値」の総和の計算(2)
これはSumProduct関数を使うと,計算もすっきりで簡単です。
![[b5]=SUMPRODUCT(B2:F2,B3:F3)](../../images/fundamental-statistics/page1/weightedmean-sub5.png)
Step 6定義式の分母・「ウエイト」の総和の計算(1)
つづいて式の分母の部分(赤い囲み)を計算します。これはウエイトの総和です。
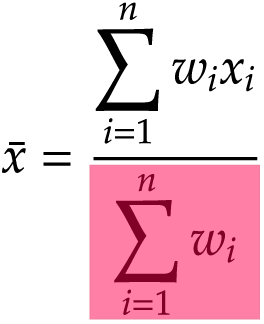
Step 7定義式の分母・「ウエイト」の総和の計算(2)
ウエイトの総和は,下図のように求めます(ここではSum関数で)。
![[b6]=SUM(B2:F2)](../../images/fundamental-statistics/page1/weightedmean-sub7.png)
Step 8「“ウエイト×観測値” の総和」÷「“ウエイト” の総和」
最後に,ウエイト×観測値の総和をウエイトで除してやります。
![[b7]=b5/b6](../../images/fundamental-statistics/page1/weightedmean-sub8.png)
Step 9加重平均・計算完了
加重平均を求めた結果,下のようになりました。
このように,すべてのウエイトが同じである場合,最初におこなったような単純な観測値の算術平均の結果と違いません。
Step 10加重平均が役に立つのは?
であれば,逆にウエイトが異なる場合こそ加重平均がハマるはずです。
たとえば,当初データを集めたときの趣旨とは外れるものの,後日もし
「ライバルチェーンYのコーヒー品目の販売構成比(人数ベース)」
の情報を入手したとします。それが具体的に,順に
20%, 30%, 25%, 15%, 10%
であることを筆者が知ったとしたら,先の平坦なウエイトを実際のところと照らしてあらためていじってみたくなりそうです。
Step 11ウエイト補正後の結果
ということでウエイトを補正した結果(下図緑色の囲み),平均はいくらか小さく変化しました(下図青色の囲み)。これは,算術平均の結果とは異なっています。
![[b7]9.85](../../images/fundamental-statistics/page1/weightedmean3.png)
Next
その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の基本統計に関連するHow-toです。

![Tex:\[\bar{x} = \frac{ \displaystyle \sum_{i=1}^n x_i }{n}\]](../../images/fundamental-statistics/page1/mean-sub1.svg)



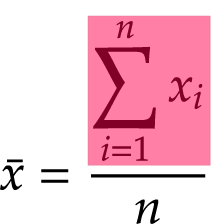

![[b15]6079.833](../../images/fundamental-statistics/page1/mean-3.svg)
![Tex:\[m_g = \sqrt[n]{ \prod_{i=1}^n x_i }\]](../../images/fundamental-statistics/page1/geomean-sub1.svg)

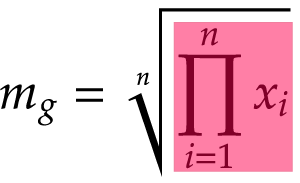
![[c15]=PRODUCT(C3:C13)](../../images/fundamental-statistics/page1/geomean-sub5.png)

![[c17]=POWER(C15,1/COUNT(C3:C13))](../../images/fundamental-statistics/page1/geomean-sub7.png)
![[c17]1.530](../../images/fundamental-statistics/page1/geomean3.svg)


![TeX: \[\bar{x} = \frac{ \displaystyle \sum_{i=1}^n w_i x_i }{ \displaystyle \sum_{i=1}^n w_i }\]](../../images/fundamental-statistics/page1/weightedmean-sub1.svg)
![[b7]11.4](../../images/fundamental-statistics/page1/weightedmean-sub8.svg)
