相関係数の計算 with Excel 3/3[スピアマンの順位相関係数]
スピアマンの順位相関係数
Step 0シチュエーションの設定
健康食品製造販売会社A社は,メインサイトの他に現在2つのウェブサイトを運営しています。その1つは情報サイトで,残る1つは物販サイトです。
Aは4週間前,両サイトにクリック保証型広告を導入しました。サイトの管理者がサイト利用者の行動分析目的でこの期間のアクセスログを確認していたとき,ふと気になったことがありました。
「当社のサイトは,平均滞在時間とCTR(Click Through Rate)とに相関があるかもしれない」
サイト管理者は早速,当該サイトの平均滞在時間(秒)とCTRの各データを抽出してみます。その結果が,下表です。
DL
:Info
DL
:EC
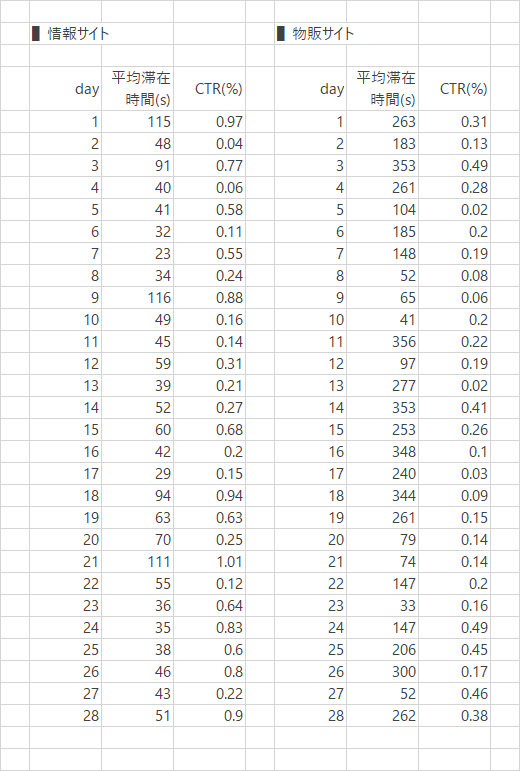
以下,これらのデータからスピアマンの順位相関係数($r_s$)を求めます。
ここでは数式をベースに一歩一歩手続きを踏んでいきます。もっともそれが面倒な場合,かつ過程がブラックボックスのままでよければ,いずれのケースも順位づけを済ませておいて,PearsonまたはCorrel関数を使えばダイレクトに結果を得ることもできます。
それもまた面倒であれば,別頁のデータをコピペするだけで計算可能なサービス「スピアマンの順位相関係数の計算 on Web」にて済ませるか,あるいは次のリンク先(外部サイト)のようなオープンなユーザー定義関数を利用するなどの手段もあります。
Step 1順位づけ(1): 同順位なし
全体の方針として,ここでは「情報サイト」「物販サイト」両データを並行して処理していくものとします。
ということで,まずは「情報サイト」の「平均滞在時間」および「CTR」値をもとに順位づけをおこなっていきたいと思います(あたらしい列を作成します)。
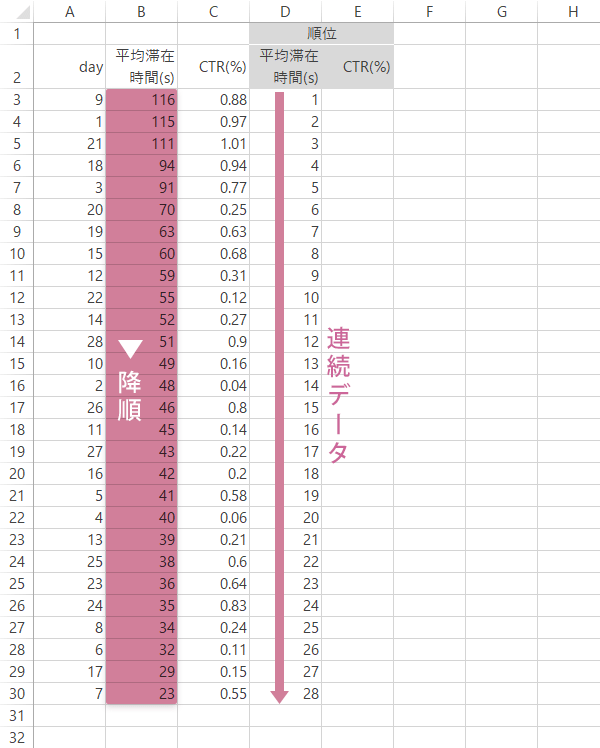
ここでは「平均滞在時間」の長い順で順位をつけていくことにします。具体的には,データを降順で並べ替え,連続データで下のように順位を振ります。
情報サイト|同順位なし
Step 2順位づけ(2): 同順位なし
つづいて「CTR」も値の大きな順で順位をつけていくことにします。先ほどと同様,データを降順で並べ替え,連続データで下のように順位を振ります。
情報サイト|同順位なし
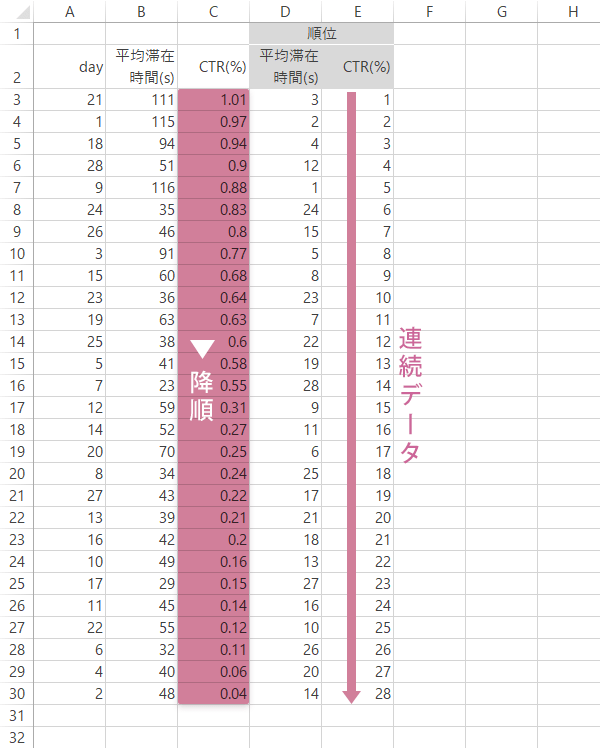
Step 3順位づけ(3): 同順位あり
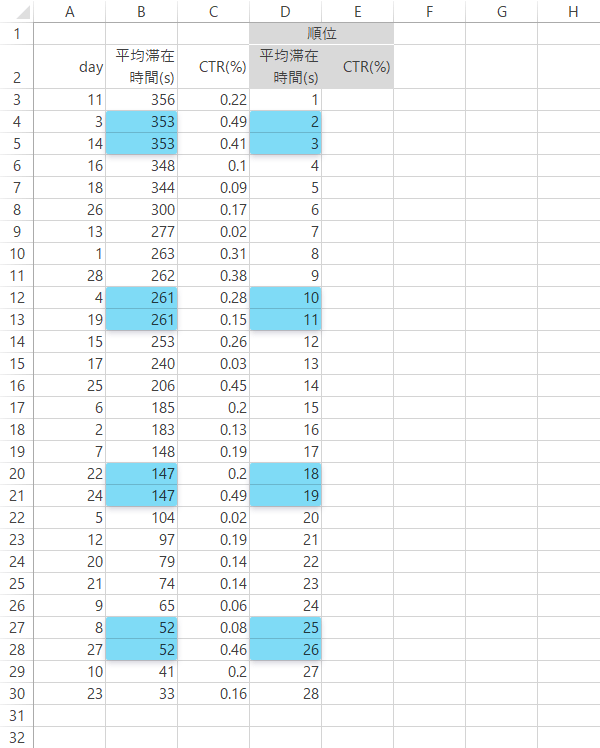
ここで対象を「物販サイト」表に移し,「平均滞在時間」および「CTR」で順位をつけたいと思います(あたらしい列を作成します)。Step 1・2と同様,「平均滞在時間」の長い順で順位をつけていくものとして,データを降順で並べ替え,連続データで順位を振ると
「平均滞在時間」の値が同値であったとしても,都合よく順位までもが同値となってはくれません。このままではしっくりこないので
物販サイト|同順位あり
Step 4順位づけ(4): 同順位あり
同じ値の場合には同じ順位が振られるよう修正を加えます。この際の順位づけのルールとして,当該部分の(修正前の)順位の和をデータの個数で割った値を用います(上表4・5行目を例とすると,(2位+3位)/2個=2.5位)。
ただし,データの数が多い場合には,1つ1つを目視しながら修正を加えていくのも手間がかかります。その場合
物販サイト|同順位あり
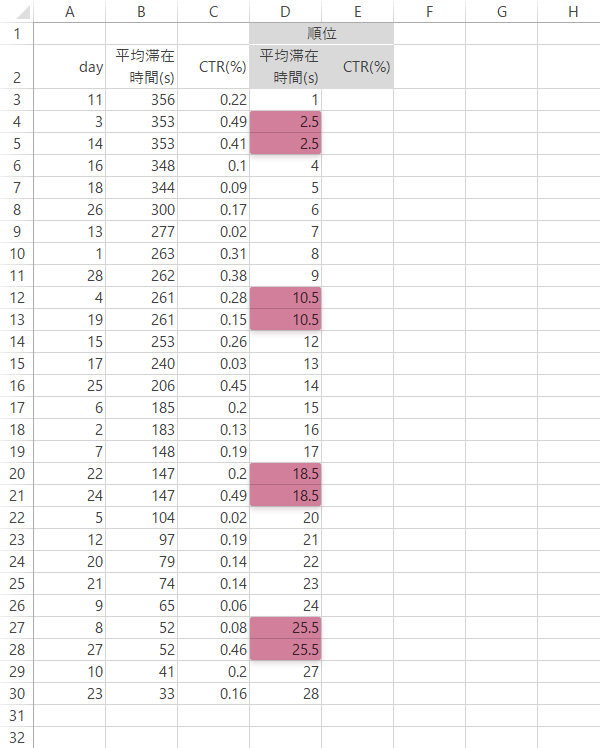
下のように,Rank.Avg関数を利用して処理すれば効率的です。
| セルD3 | =RANK.AVG(B3, \$B\$3:\$B\$30, 0) |
|---|
Step 5順位づけ(5): 同順位あり
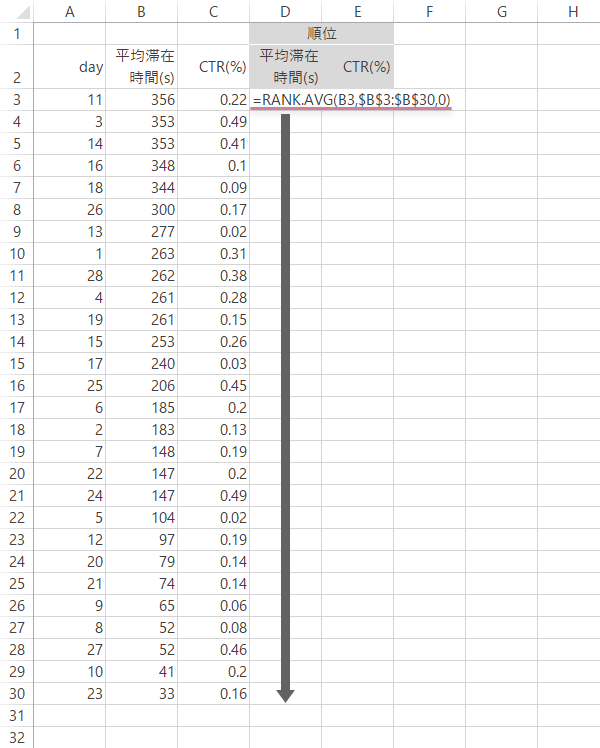
「CTR」も同じようにして降順でデータを並べ替え,連続データを振ったのち修正を加えるか,あるいはダイレクトにRank.Avg関数を使ってするかして順位をつくります(下の表は順位を振った後の値)。
| セルE3 | =RANK.AVG(C3, \$C\$3:\$C\$30, 0) |
|---|
物販サイト|同順位あり
Step 6スピアマンの順位相関係数の計算(1): 同順位なし
「情報サイト」の$r_s$を求めます。同順位のない場合,計算式は次のとおりです。
$n$: データ対の数,$d$: 順位の差; より丁寧に言えば変数$X$の$i$番目の要素の順位($rank$)と変数$Y$の$i$番目の要素の順位の差[$rank(X_i)-rank(Y_i)$]。
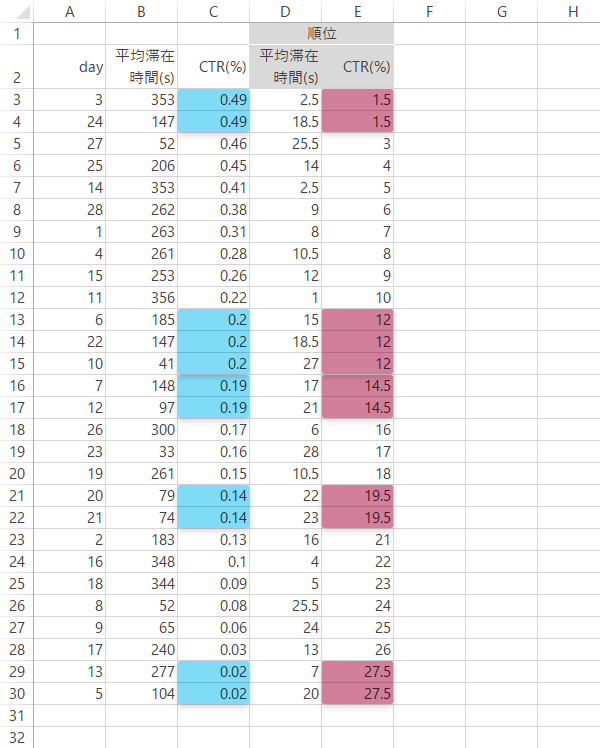
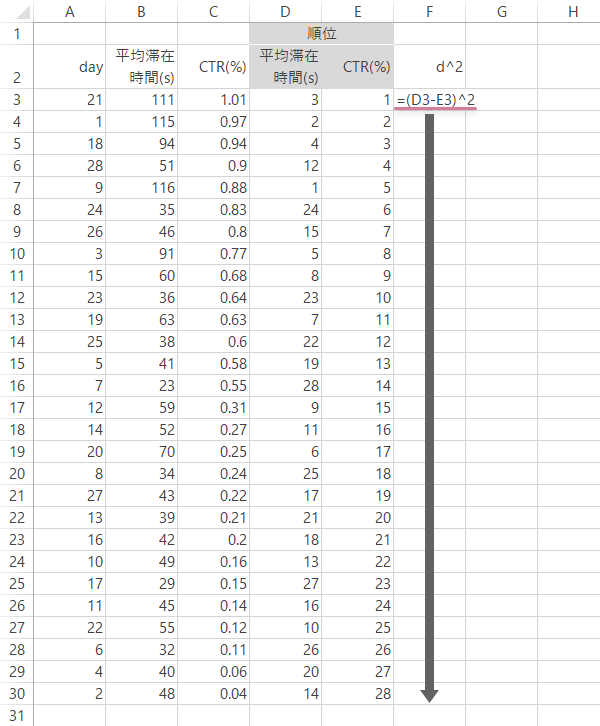
準備として,式の$d^2 _i$を求めるための領域をあらたに用意します(F列)。この見出しの直下のセルに両順位の差の2乗を求める式
| セルF3 | =(D3-E3)^2 |
|---|
を入力し,コピーします。
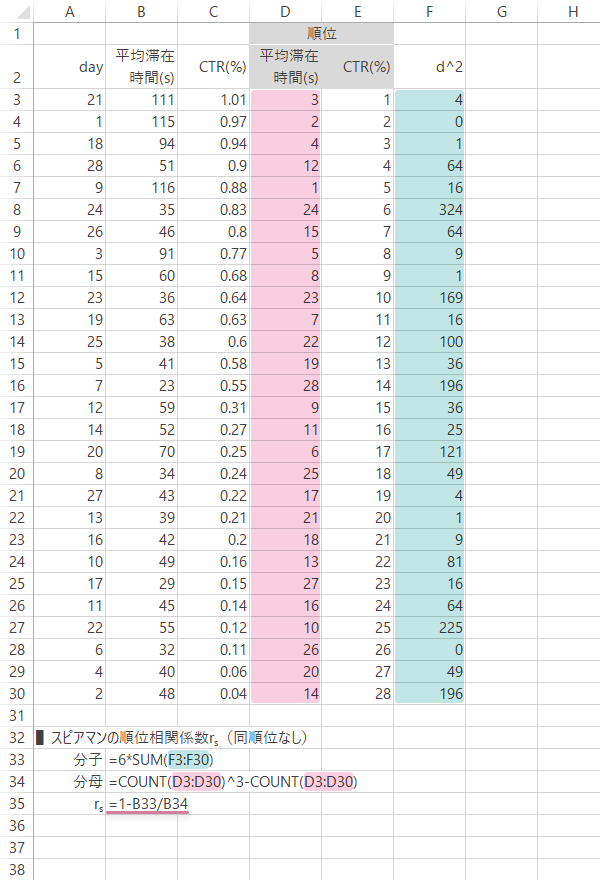
情報サイト|同順位なし
Step 7スピアマンの順位相関係数の計算(2): 同順位なし
任意のセルで$r_s$を求めます。
Excel式が複雑化するのを避ける目的から,ここではStep 6式を,
| 分子(セルB33) | =6*SUM(F3:F30) |
|---|---|
| 分母(セルB34) | =COUNT(D3:D30)^3-COUNT(D3:D30) |
と分けて入力しています。これらの値から,目的の相関係数($r_s$)が求められます。
| rs(セルB35) | =1-B33/B34 |
|---|
情報サイト|同順位なし
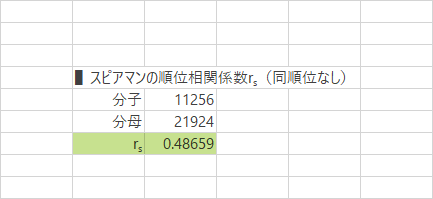
Step 8スピアマンの順位相関係数(同順位なし)・計算完了
情報サイトの$r_s$は0.49となりました。
情報サイト|同順位なし
Step 9スピアマンの順位相関係数の計算(1): 同順位あり
対象を再び移し,同順位のある「物販サイト」の$r_s$を求めます。なお説明の都合,以下では便宜的に「順位:平均滞在時間」を“変数$X$”,「順位:CTR」を“変数$Y$”と呼ぶことにします。
同順位のある場合,次の式で$r_s$を求めます。
$n$: データ対の数,$d$: 順位の差; より丁寧に言えば変数$X$の$i$番目の要素の順位($rank$)と変数$Y$の$i$番目の要素の順位の差[$rank(X_i)-rank(Y_i)$]。
このとき,$T_X$, $T_Y$の内容はそれぞれ次のとおりです。
$X_R$: 変数$X$の同順位の組の数,$Y_R$: 変数$Y$の同順位の組の数,$t_i$: 変数$X$の$i$番目の同順位の組について,そのデータの数,$t_j$: 変数$Y$の$j$番目の同順位の組について,そのデータの数。
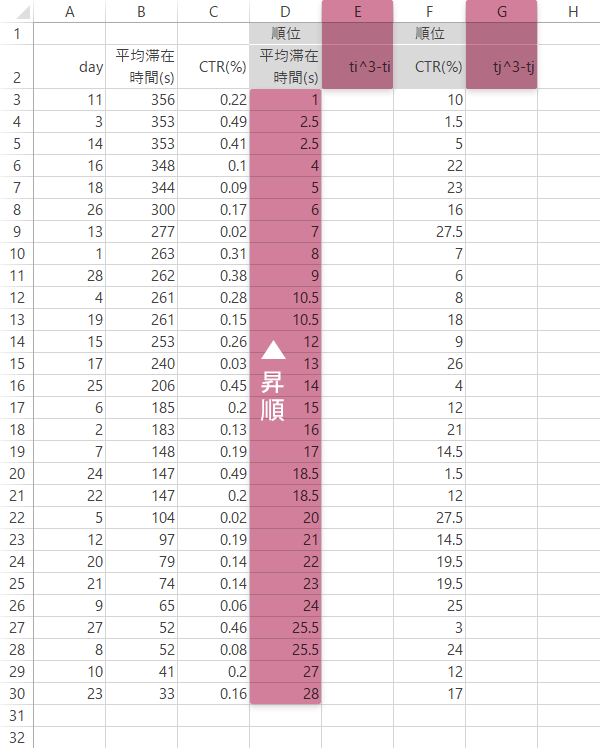
Step 10スピアマンの順位相関係数の計算(2): 同順位あり
ここで変数$X$の昇順でデータを並べ替えます。
つづいてE列にあたらしい列を挿入し,E・G列に下のような見出しを作成します。この両列はStep 9式・$T_X$,$T_Y$の$\sum$を計算するために使います。
物販サイト|同順位あり
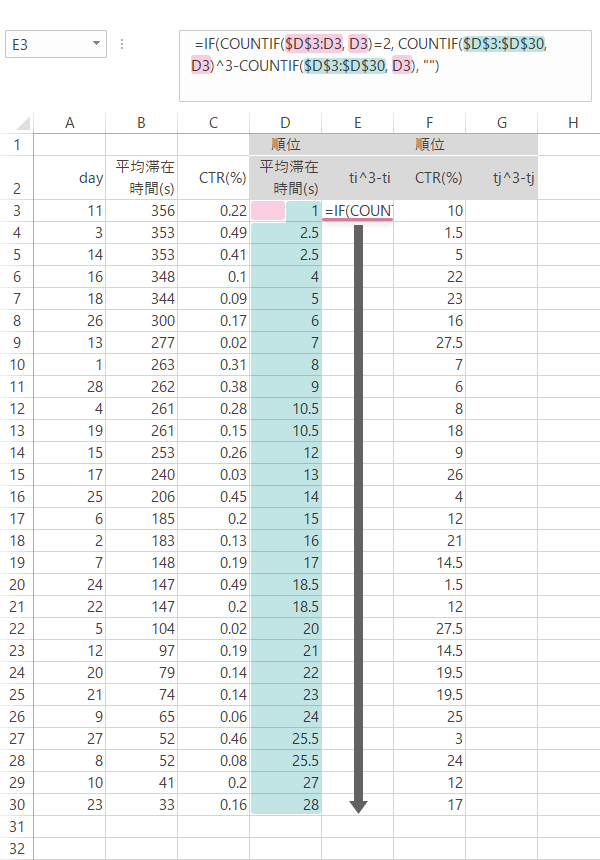
Step 11スピアマンの順位相関係数の計算(3): 同順位あり
「物販サイト」の変数$X$については,同順位の組が4つあります。したがって,$i=$1~4の各組の$t^3-t$を求めます。4組ともにそれぞれ2個のデータからなるので,$t$はすべて2として計算します。
ただ,この計算も先と同様,数が多いと手間がかかります。ということで,関数を使って同順位の中でも2番目に登場するデータ行にのみ自動で計算させてもいいかと思います(下図)。
| セルE3 | =IF(COUNTIF(\$D\$3:D3, D3)=2, COUNTIF(\$D\$3:\$D\$30, D3)^3-COUNTIF(\$D\$3:\$D\$30, D3), "") |
|---|
物販サイト|同順位あり
Step 12スピアマンの順位相関係数の計算(4): 同順位あり
「物販サイト」の変数$Y$(「順位:CTR」)についてもStep 11の操作を繰り返します($j=$1~5の各組の$t^3-t$の計算; 並べ替えておくと確認しやすいと思います)。
念のため,こちらは(下のように並べ替えたとき)上から2番目の組,つまり$t_2$のみ3となっていることがわかります。Step 11と同様関数を利用する場合には,COUNTIF関数の引数に変数$Y$(「順位:CTR」)を指定します。
| セルG3 | =IF(COUNTIF(\$F\$3:F3, F3)=2, COUNTIF(\$F\$3:\$F\$30, F3)^3-COUNTIF(\$F\$3:\$F\$30, F3), "") |
|---|
物販サイト|同順位あり
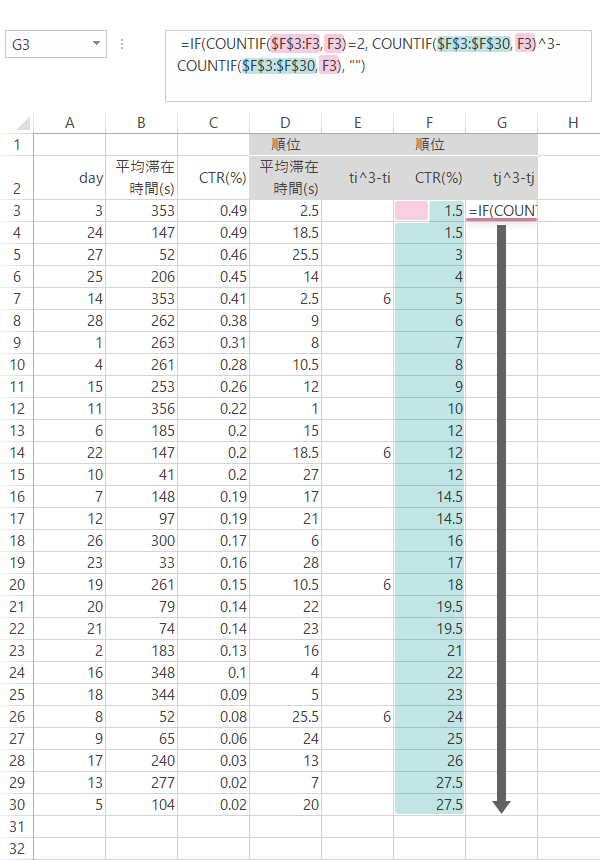
Step 13スピアマンの順位相関係数の計算(5): 同順位あり
下図のようにあらたな見出しを作成します。なお$n$のみあらかじめ入力or計算しておきます(ここでは28)。
物販サイト|同順位あり
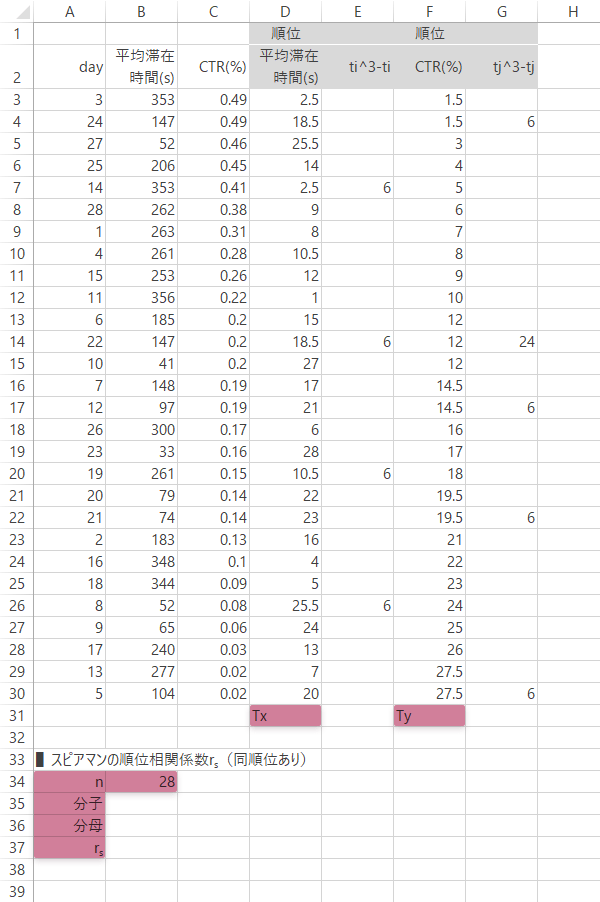
Step 14スピアマンの順位相関係数の計算(6): 同順位あり
Step 9式にしたがって$T_X$,$T_Y$を求めます。ここでは,
| TX(セルE31) | =(B34^3-B34-SUM(E3:E30))/12 |
|---|---|
| TY(セルG31) | =(B34^3-B34-SUM(G3:G30))/12 |
となります。
物販サイト|同順位あり
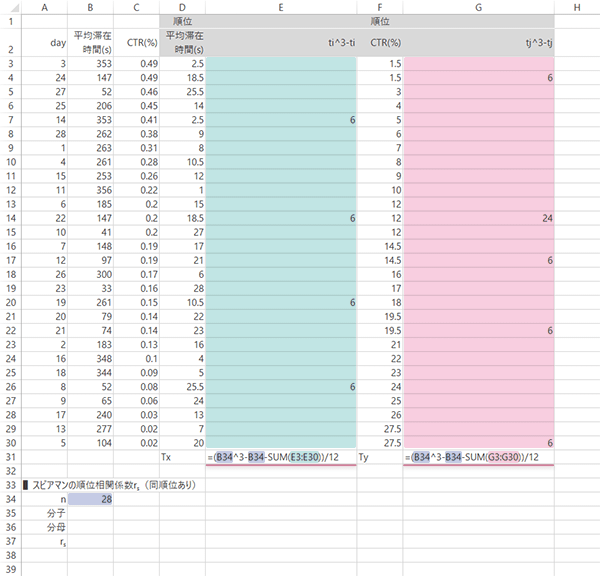
Step 15スピアマンの順位相関係数の計算(7): 同順位あり
2変数の順位の差の2乗$d^2_i$を計算します。
ここではH列で計算します。見出しの直下のセルに
| セルH3 | =(D3-F3)^2 |
|---|
と入力し,表の最下行までコピーします。
物販サイト|同順位あり
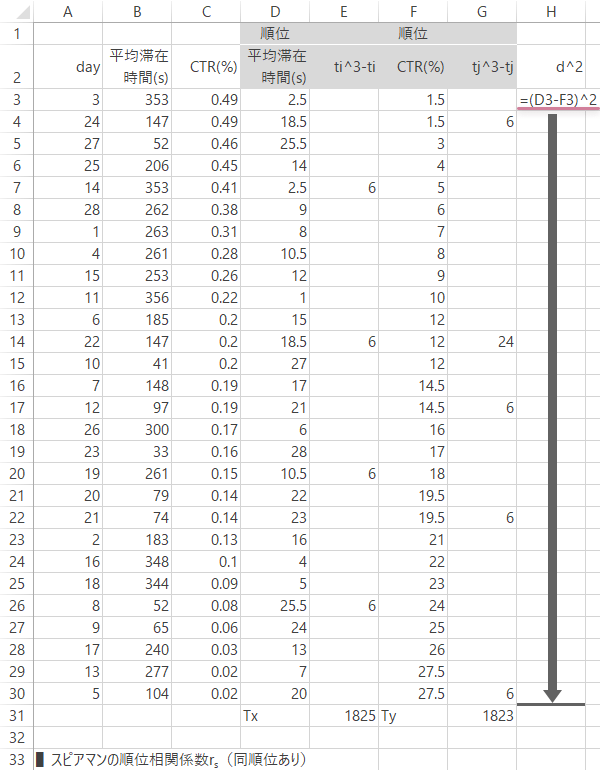
Step 16スピアマンの順位相関係数の計算(8): 同順位あり
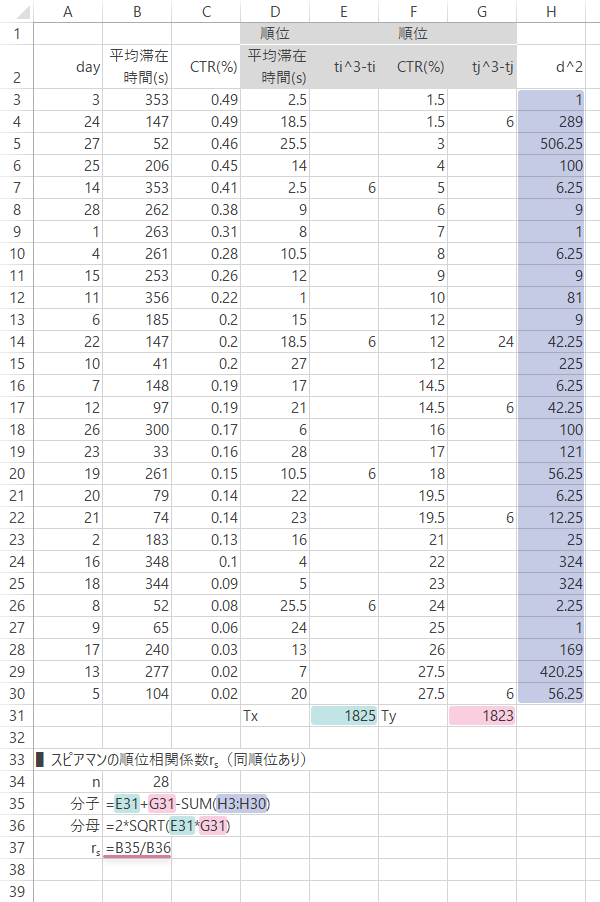
Step 9式にしたがって,「物販サイト」の$r_s$を求めます。先と同様Excel式が複雑化するのを避ける目的から,ここでは,
| 分子(セルB35) | =E31+G31-SUM(H3:H30) |
|---|---|
| 分母(セルB36) | =2*SQRT(E31*G31) |
と分けて入力しています。これらの値から,目的の相関係数($r_s$)が求められます。
| rs(セルB37) | =B35/B36 |
|---|
物販サイト|同順位あり
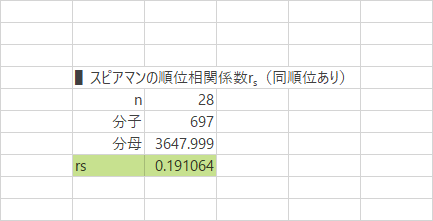
Step 17スピアマンの順位相関係数(同順位あり)・計算完了
物販サイトの$r_s$は0.19となりました。
なお$r_s$は,同順位のある・ない,いずれの場合も-1から1の値をとります。2変数の関連についての考え方は,ピアソンの積率相関係数と同じです。
物販サイト|同順位あり
Step 18無相関検定をおこなう場合
$n$がある程度大きな場合(目安として>30),検定はピアソンの積率相関係数と同様の手続きでおこなえます($t$検定。ただし統計パッケージやアドインなどによって,これと異なる方法が用いられることも)。細説が必要であれば,メインサイト「散布図の作成と相関係数の計算(相関分析) with Excel」頁を参照ください。
また$n$が小さな場合は,下のような$r_s$の有意点を示す検定表をもとに判断します。たとえば$n=10$で両側5%検定をおこなう場合,少なくとも$r_s$が0.649ないと帰無仮説を棄却することができません。
| 両側検定の有意水準 | |||
| n | 0.1 | 0.05 | 0.01 |
| 5 | 0.900 | 1.000 | - |
| 6 | 0.829 | 0.886 | 1.000 |
| 7 | 0.715 | 0.786 | 0.929 |
| 8 | 0.620 | 0.715 | 0.881 |
| 9 | 0.600 | 0.700 | 0.834 |
| 10 | 0.564 | 0.649 | 0.794 |
| 11 | 0.537 | 0.619 | 0.764 |
| 12 | 0.504 | 0.588 | 0.735 |
| 13 | 0.484 | 0.561 | 0.704 |
| 14 | 0.464 | 0.539 | 0.680 |
| 15 | 0.447 | 0.522 | 0.658 |
| 16 | 0.430 | 0.503 | 0.636 |
| 17 | 0.415 | 0.488 | 0.618 |
| 18 | 0.402 | 0.474 | 0.600 |
| 19 | 0.392 | 0.460 | 0.585 |
| 20 | 0.381 | 0.447 | 0.570 |
[上表の引用元]岸・吉田(2010), p.290.
参考にした書籍およびWebページ
- 岸 学・吉田裕明(2010)『ツールとしての統計分析 ―Excelの基本からデータ入力・集計・分析まで―』オーム社, pp.151-156.
- 上田拓治(2009)『44の例題で学ぶ統計的検定と推定の解き方』オーム社, pp.146-148.
- [Web]スピアマンの順位相関係数 ―"Wikipedia"(2013.7.閲覧)
$r_s$を計算できるExcelアドインソフト
- エクセル統計 BellCurve
- 「基本統計・相関」「スピアマン(Spearman)の順位相関行列」(別にケンドール(Kendall)の順位相関係数にも対応)
- Statcel4(4Stepsエクセル統計)
- 「ノンパラメトリック検定」「スピアマンの順位相関係数検定」
その他の参照
メインサイト「ひとりマーケティングのためのデータ分析」の相関に関するHow-toです。