相関係数の計算 with Excel 1/3[クラメールの連関係数]
クラメールの連関係数・相関比・スピアマンの順位相関係数
ここでは,ピアソンの積率相関係数(数量データ×数量データ)以外のさまざまな相関係数を求めます。最初に,カテゴリデータ×カテゴリデータの場合に用いるクラメールの連関係数(このページ)を,次に数量データ×カテゴリデータの場合の相関比を,そして最後に順序尺度に関するスピアマンの順位相関係数をExcelで計算します。
相関係数の計算
クラメールの連関係数
Step 0シチュエーションの設定
東日本と西日本の境界を隔てるA地域とM地域にいくつかの店舗をもつ飲食店Xがあります。このたびXでは,提供する料理の風味が従来品とは異なるSを,新メニューとして採用することを検討しています。ただ,両地域での画一的な商品展開には,嗜好の違いも想定されることから躊躇されるところもあります。
そこでXでは判断の一端として,現場の全ての従業者の感覚を大切にしてみたいと考えました。勤務シフトの異なる多忙な従業者に対し,一定の期限までに都合のついた最低限の質問は次の1点です。
- 商品Sが地域の顧客に受容されると思うか(おおいに・ふつう・まったく)
この質問に対する回答を,地域別にクロス集計したものが次の表です。
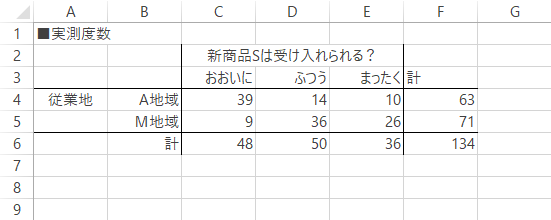
一瞥したところ,従業地と受容についての予測には関連が見られそうです。
そこで,Xではこれがどの程度のものか,指標として確かめてみたいと考えました。以下,このデータをもとにクラメールの連関係数($V$)を求めます。
Step 1準備
「実測度数」表の直下に,下図と同様の表組みを作成します。中段の表は期待度数を,下段のそれはピアソンの\(\chi^2\)(カイ2乗, 以下に同じ)を求めるために利用します。
またこれらと合わせて「\(\chi^2\)」「クラメールの連関係数」の各見出しも用意しておきます。
DL

Step 2期待度数を求める(1)
「期待度数」表のデータ範囲にいう最も左上のセルに,下の式を入力します。
| セルC11 | =\$F4*C\$6/\$F\$6 |
|---|
この式は,「実測度数」表に関して
当該行計 × 当該列計 ÷ 総計
を求めます(複合参照するセルと絶対参照するセルがあります)。
これにより,関連がまったくないと仮定したときの,総人数(総度数; ここでは134人)に占めるであろう各セルの人数(たとえば,セルC11であれば「A地域」[63/134]であって回答が「おおいに」[48/134]である人の数[(63*48)/134])を求めることができます。
入力したのち,これを「期待度数」表すべてのデータ範囲にコピーします。
![[セルC11]=$F4*C$6/$F$6](../../images/correlation-coefficient/cramer/step2.png)
Step 3期待度数を求める(2)
「期待度数」表の,下図彩色部分を選択した状態でオートサムボタン(Σ)をクリックし,行計・列計を一度に求めます。
![[選択範囲]C11:F13](../../images/correlation-coefficient/cramer/step3.png)
Step 4ズレをはかる(1)
「ズレ」表のデータ範囲・最も左上のセルに,下の式を入力します。
| セルC18 | =(C4-C11)^2/C11 |
|---|
両表で相対するセルの差の2乗をとって先の期待度数で除し,実測・期待両度数の“ズレ”をはかります(ピアソンの\(\chi^2\)の計算式の一部)。
入力したのち,これも先と同じように同表すべてのデータ範囲にコピーします。
![[セルC18]=(C4-C11)^2/C11](../../images/correlation-coefficient/cramer/step4.png)
Step 5ズレをはかる(2)
「ズレ」表の下図彩色部分を選択した状態でオートサムボタン(Σ)をクリックし,行計・列計を一度に求めます。
![[選択範囲]C18:F20](../../images/correlation-coefficient/cramer/step5.png)
Step 6ズレを足し合わせて χ2 統計量を求める
「ズレ」表の下図彩色部分が\(\chi^2\)統計量です。
より明示的に,ここではこれを表の直下に転記したいと思います。
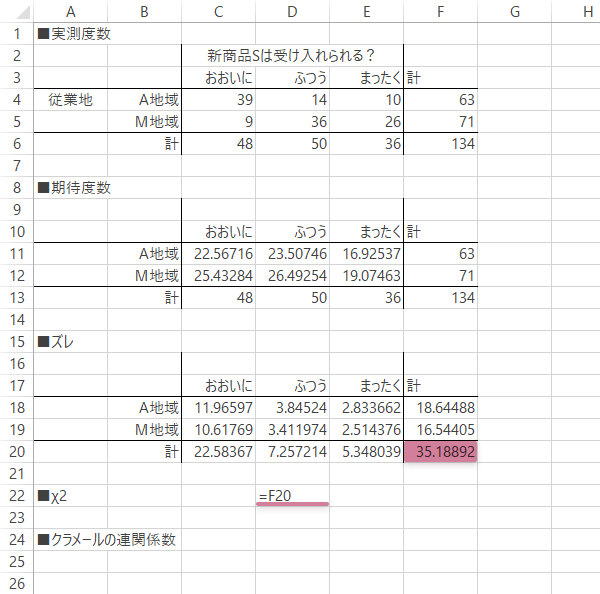
Step 7クラメールの連関係数の計算
\(\chi^2\)統計量をもとに$V$を計算します。これは次の式で求めることができます。
$n$: 総度数,$k$: クロス集計表の行数,$l$: クロス集計表の列数。
この式をExcelの計算式として下式のように落とし込みます。
| セルD24 | =SQRT(D22/(F6*(MIN(2, 3)-1))) |
|---|
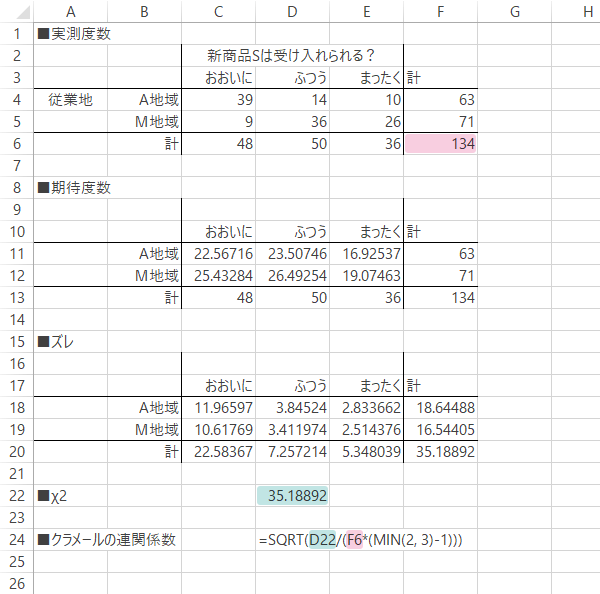
Step 8クラメールの連関係数・計算完了
$V$は0.51となりました。
なお$V$は,0から1の値をとります。2変数の関連において,0に近いほど弱く,1に近いほど強いと考えます。

参考にした書籍
- 岸 学・吉田裕明(2010)『ツールとしての統計分析 ―Excelの基本からデータ入力・集計・分析まで―』オーム社, pp.160-164.
- 高橋 信(2004)『マンガでわかる統計学』オーム社, pp.127-136.
Next
$V$を計算できるExcelアドインソフト
- エクセル統計 BellCurve
- 「集計表の作成と分析」「クロス集計表の作成と分析」「独立性の検定」他における出力項目
- Statcel4(4Stepsエクセル統計)
- 「分割表の検定」「m×n 分割表」における出力項目
その他の参照
メインサイト「ひとりマーケティングのためのデータ分析」の相関に関するHow-toです。