母比率の信頼区間の推定 with Excel
Step 0Case 1 - 2 共通の設定
この頁では推定にあたり,
- 標本サイズ$n$が大きいか小さいか(:中心極限定理)
を判断し,前者の場合で標準正規分布($z$分布)を,後者の場合で$F$分布を利用します。
ショートカット
- $z$推定(大標本[$n\geqq30$])
- $F$推定(小標本[$n<30$])
大標本のときのz推定
Case 1-Step 0シチュエーションの設定
スナック菓子製造X社は,新商品のパッケージデザインについて,社内評価の高いものから順にA~Dの4つの案を持っています。X社は今のところ社内受けのよいA案を採用したいと考えていますが,限られた範囲の評価で不安もあります。そこでこの商品のメインターゲット層に対し,あらためて反応を探ってみることになりました。
具体的には,ターゲットとなる特定の属性の女性30人(ここでは無作為の抽出と仮定します)に,A~Dについて支持できるデザインを1つだけ選択してもらうといった調査をおこないました。下の表がその結果です。
このデータから,メインターゲット層のデザインAに関する支持率の区間推定をおこないます。結果,信頼度80%で下側信頼限界が50%を超えてくるようであれば,X社はデザインAを採用する方針です。
Case 1-Step 1前提
$n\geqq30$を満たすことから,これを
- 大標本
と判断します(これは一意な基準ではありません[以下Caseに同じ])。
したがってCase 1ではStep 0の方針と照らし,
標準正規分布($z$分布)
を利用します。
Case 1-Step 2見出しの入力
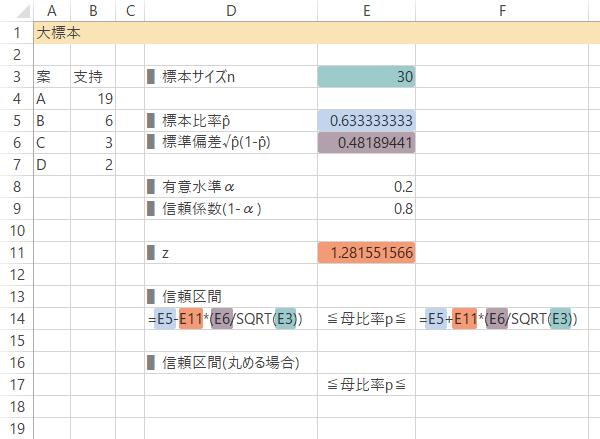
母比率$p$の信頼区間は次の式によって求められます。
ただし, $\widehat{p}$: 標本比率, $\sqrt{\widehat{p}(1-\widehat{p})}$: 標準偏差, $z(\alpha/2)$: 標準正規分布の上側$\alpha/2$パーセント点。
これをシート上で計算するため,下表のような見出しを作成しておきます。

Case 1-Step 3p̂, n, √p̂(1-p̂) の入力または計算
$n$(セルE3),およびA案についての$\widehat{p}$(セルE5)を求めます。
あわせて$\sqrt{\widehat{p}(1-\widehat{p})}$も求めておきます(セルE6)。
![[セルE3]=SUM(B4:B7), [セルE5]=B4/E3, [セルE6]=SQRT(E5*(1-E5))](../../images/confidence-interval/population-ratio/case1/step3.png)
Case 1-Step 4信頼係数の決定
(仮に)同様の標本抽出から区間推定を繰り返しおこなうことを考えたとき,その繰り返しのなかで一定の幅をもつ区間に母比率$p$を捉えられるであろう割合(「信頼係数」)を定めます。一般には0.90・0.95・0.99(百分率での表記の場合,これらを順に“信頼度”90%・95%・99%とも)といったところが利用されます。信頼係数を大きくとれば,区間の幅も広くなります。
ここでは設定のとおり,上記の羅列にはない0.80(80%)を選択します。これにより,有意水準(過誤確率)も決まります(1-信頼係数)。
![[セルE8]=1-E9, [セルE9]0.8](../../images/confidence-interval/population-ratio/case1/step4.png)
Case 1-Step 5zの入力または計算
標準正規分布の上側$\alpha/2$パーセント点を計算または入力します(下は計算の例です)。ExcelのNORM.S.INV関数は累積(下側)確率$p$に対する$z$の値を返すので,上側$z$はNORM.S.INV($\alpha/2$+信頼係数)で計算します。つまり,信頼係数を0.80とした場合,$p=0.90$として対応する$z$を求めることになります。
![[セルE11]=NORM.S.INV(E8/2+E9)](../../images/confidence-interval/population-ratio/case1/step5.png)
また直接入力する場合,標準正規分布表から上側$\alpha/2$に対応する$z$を読み取ります。たとえば先に上げた3つ+今回利用の信頼係数に対応する上側$z$は,下の表のとおりです。
| 0.80($\alpha/2=0.10$) | 1.28 |
|---|---|
| 0.90($\alpha/2=0.05$) | 1.64 |
| 0.95($\alpha/2=0.025$) | 1.96 |
| 0.99($\alpha/2=0.005$) | 2.58 |
Case 1-Step 6信頼区間の計算
Case 1-Step 7信頼区間の計算(桁をくり上げる場合)
任意の桁で丸めるときは,信頼区間を満たすよう 下は切り捨て・上は切り上げによって処理します。
| 下側 | =ROUNDDOWN(D14, 3) |
|---|---|
| 上側 | =ROUNDUP(F14, 3) |
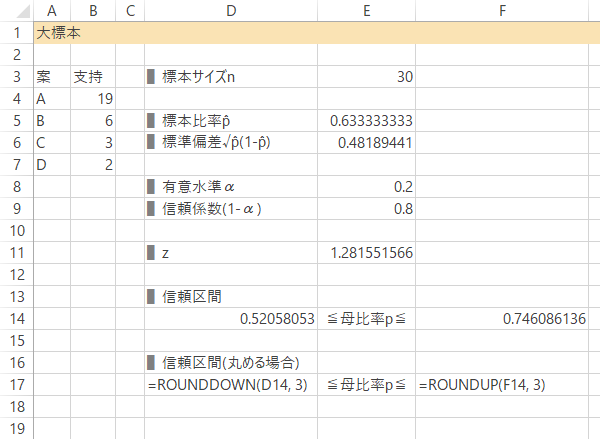
結果: メインターゲット層の支持に関して,信頼度80%のとき下側信頼限界は50%をこえることが確認できます。
Case 1-Step 8専用の関数を使うなら
上述の経過をブラックボックスにしてもよいのなら,CONFIDENCE.NORM関数によっても同様の計算が可能です。
![[セルE13]=CONFIDENCE>NORM(E8,E6,E3), [セルD16]=E5-E13, [セルF16]=E5+E13](../../images/confidence-interval//population-ratio/case1/step8.png)
| 1/2区間 | =CONFIDENCE.NORM(α, √p̂(1-p̂), n) |
|---|
この場合,戻り値は区間の幅の半分(1/2)です。これを$\widehat{p}$に加減して上限・下限を求めます。
小標本のときのF推定
Case 2-Step 0シチュエーションの設定
ある大学の大学祭実行委員会は,この年の成功を左右するイベント“企画A”を学生に対し積極的にPRしています。
周知期間をいくらか経たのち,さらに周知を続けるべきかが議論され,結局,効果を測定してから判断しようという方針になりました。そこで,無作為に抽出した20人の学生に対し,企画Aを知っているか聞き取りをおこなった結果が下の表です(○:既知, ×:未知)。
このデータから,現時点における企画Aの認知度の区間推定をおこないます。
Case 2-Step 1前提
Case 2-Step 2見出しの入力
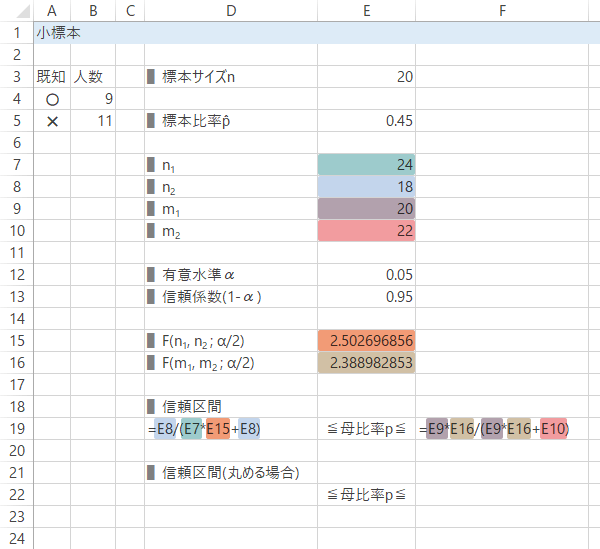
母比率$p$の信頼区間は次の式によって求められます。
ただし,
- $n_1=2n(1-\widehat{p})+2$
- $n_2=2n\widehat{p}$
- $m_1=2n\widehat{p}+2$
- $m_2=2n(1-\widehat{p})$
$\widehat{p}$: 標本比率。また, $F(n_1, n_2; \alpha/2)$: 自由度$n_1$, $n_2$の$F$分布の上側$\alpha/2$パーセント点, $F(m_1, m_2; \alpha/2)$: 自由度$m_1$, $m_2$の$F$分布の上側$\alpha/2$パーセント点。
これをシート上で計算するため,下表のような見出しを作成しておきます。
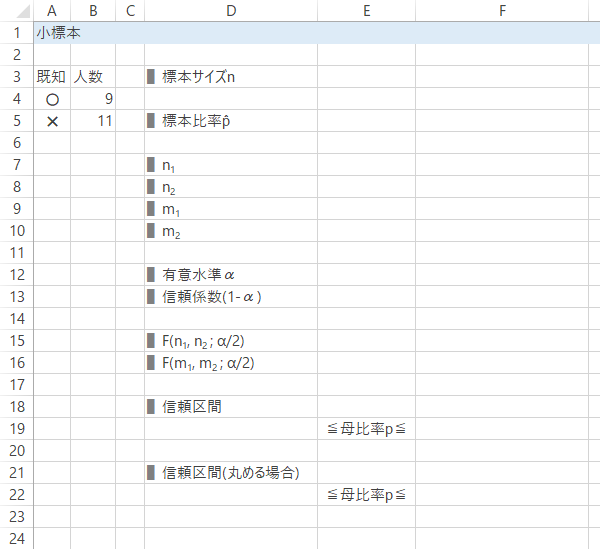
Case 2-Step 3p̂, n, 自由度n1~m2 の入力または計算
$n$(セルE3),$\widehat{p}$(セルE5)を求めます。
また$n_1, n_2, m_1, m_2$についても求めておきます(セルE7:E10)。
![[セルE3]=SUM(B4:B5), [セルE5]=B4/E3, [セルE7]=2*E3*(1-E5)+2, [セルE8]=2*E3*E5, [セルE9]=2*E3*E5+2, [セルE10]=2*E3*(1-E5)](../../images/confidence-interval/population-ratio/case2/step3.png)
Case 2-Step 4信頼係数の決定
(仮に)同様の標本抽出から区間推定を繰り返しおこなうことを考えたとき,その繰り返しのなかで一定の幅をもつ区間に母比率$p$を捉えられるであろう割合(「信頼係数」)を定めます。一般には0.90・0.95・0.99(百分率での表記の場合,これらを順に“信頼度”90%・95%・99%とも)といったところが利用されます。信頼係数を大きくとれば,区間の幅も広くなります。
ここでは0.95(95%)を選択します。これにより,有意水準(過誤確率)も決まります(1-信頼係数)。
![[セルE12]=1-E13, [セルE13]0.95](../../images/confidence-interval/population-ratio/case2/step4.png)
Case 2-Step 5Fの計算
自由度$n_1,n_2$,$m_1,m_2$それぞれの$F$分布の上側$\alpha/2$パーセント点を計算します。F.INV.RT関数は上側確率$p$に対する$F$の値を返すので,F.INV.RT($\alpha/2$, 第1自由度, 第2自由度)として計算します。 つまり,信頼係数を0.95とした場合,$p=0.025$として対応する$F$を求めることになります。
![[セルE15]=F.INV.RT(E12/2,E7,E8), [セルE16]=F.INV.RT(E12/2,E9,E10)](../../images/confidence-interval/population-ratio/case2/step5.png)
Case 2-Step 6信頼区間の計算
Case 2-Step 7信頼区間の計算(桁をくり上げる場合)
任意の桁で丸めるときは,信頼区間を満たすよう 下は切り捨て・上は切り上げによって処理します。
| 下側 | =ROUNDDOWN(D19, 2) |
|---|---|
| 上側 | =ROUNDUP(F19, 2) |
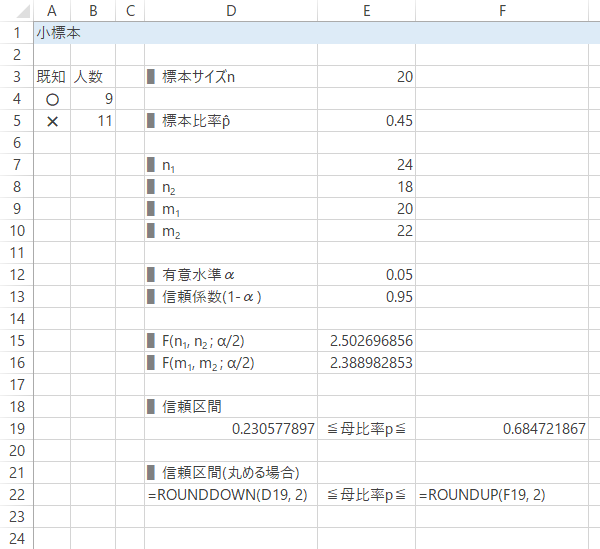
結果: 企画Aの学生の認知度$p$は,信頼度95%で23~69%の間にあると考えられます。
参考にした書籍
- 上田拓治(2009)『44の例題で学ぶ統計的検定と推定の解き方』オーム社, pp.179-183.
- 栗原伸一(2011)『入門 統計学 -検定から多変量解析・実験計画法まで-』オーム社, pp.72-77.
- 石村光資郎(2012)『身近な事例で学ぶやさしい統計学』オーム社, pp.114-118.
- アミール D. アクゼル・ジャヤベル ソウンデルパンディアン(2007)『ビジネス統計学[上]』鈴木一功監訳, 手嶋宣之・原 郁・原田喜美枝訳, ダイヤモンド社, pp.290-294.
母比率の推定に対応するexcelアドインソフト
- エクセル統計 BellCurve
- 「1標本の推定と検定」「母比率の推定」($z$推定・$F$推定|有限母集団修正も可能)
その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の有意性検定に関するHow-toです。