F分布の確率とパーセント点の計算 with Excel
Step 0シチュエーションの設定
ここでは,下のようなF分布表(上側確率5%,1.-Step3のみ95%表を使用)を使って確率あるいはFの値を求める作業を,Excelでの処理に置き換えて見ていきます。
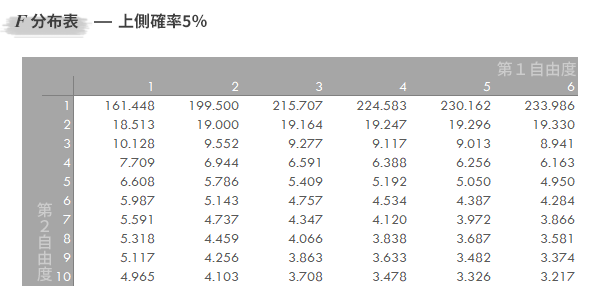
以下共通の設定として,第1自由度を5,第2自由度を10と固定して進めます。
F から 確率p を求める
Step 1ある F の値より大きくなる確率上側確率p
F=3.326のときの,下のF分布表にいう左上ハイライトの部分に相当する値を求めます。
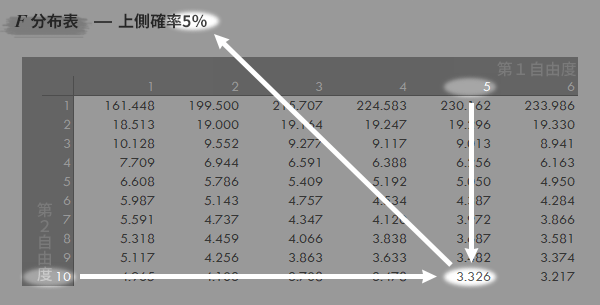
Step 2F.DIST.RT, F.DIST関数
上側確率は,ExcelではF.DIST.RT関数で求めます。この場合の引数は次のとおりです。
- F.DIST.RT(F, 第1自由度, 第2自由度) ―"Office"
具体的には,下図・下表のような式で上側確率が求められます。

| B7 | =F.DIST.RT(B4, B1, B2) |
|---|
他方,これは次の関数を使って求めることも可能です。
- F.DIST(F, 第1自由度, 第2自由度, 関数形式※)
※引数「関数形式」は,[true] の指定で下側(累積)確率が,[false] の指定で確率密度(高さ)が返ります(ここでは後者の指定を必要とするような手続きは登場しません)。
この場合,具体的な式は下図・下表のようになります。
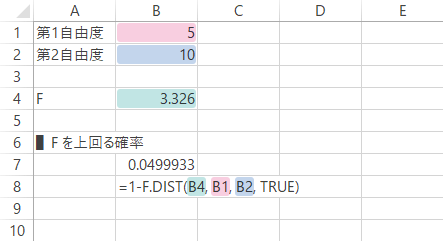
| B8 | =1-F.DIST(B4, B1, B2, TRUE) |
|---|
戻り値: 0.050(5%)[※少数点第4位で四捨五入。以下に同じ]。これは,下のグラフ[※イメージ。以下に同じ]のグレーの彩色部分の面積です。
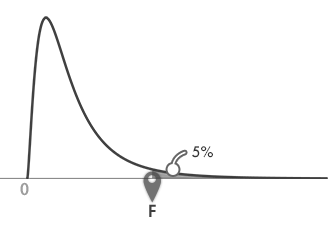
Step 3ある F の値より小さくなる確率下側確率p
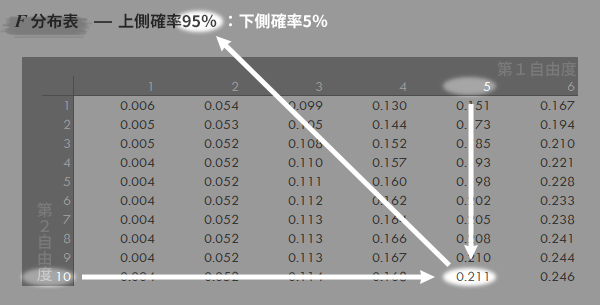
F=0.211のとき,下の F分布表(上側確率95%, 例示のため変則的に作成したもの)において下側確率は0.050 (5%; =1-0.95)とわかります(左上のハイライトの部分)。
Step 4F.DIST.RT, F.DIST関数
こちらも上側と同様に,F.DIST.RT関数で求められます。
具体的には,下図・下表のようになります。

| B7 | =1-F.DIST.RT(B4, B1, B2) |
|---|
またこれは,先と同様F.DIST関数を利用して求めることも可能です。
この場合の式は下図・下表のとおりです。
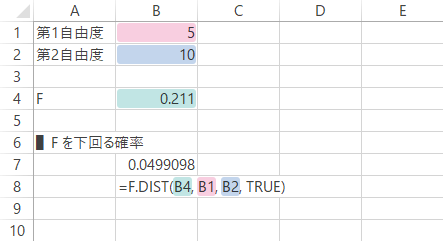
| B8 | =F.DIST(B4, B1, B2, TRUE) |
|---|
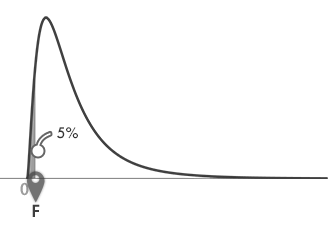
戻り値: 0.050(5%)。これは,下のグラフのグレーの彩色部分の面積です。
片側確率p(上or下) から F を求める[パーセント点]
Step 1上側確率p のときの F
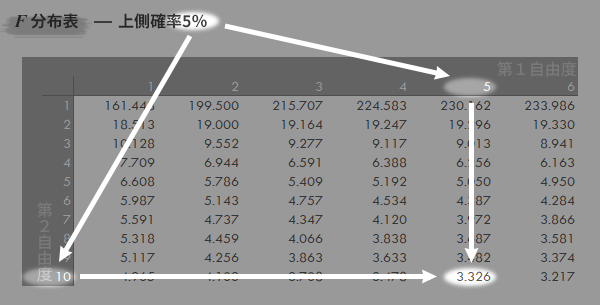
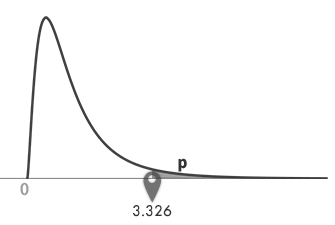
上側p=0.05のとき,F分布表においてFは3.326とわかります(下図矢印の参照)。
Step 2F.INV.RT, F.INV関数
上側pに対するFの値(100×pパーセント点)は,F.INV.RT関数で求めます。このとき,引数は次のとおりです。
- F.INV.RT(上側p, 第1自由度, 第2自由度) ―"Office"
具体的には,下図・下表のような式でFが求められます。

| B7 | =F.INV.RT(B4, B1, B2) |
|---|
他方,これは次の関数を使って求めることも可能です。
- F.INV(下側p, 第1自由度, 第2自由度)
この場合,具体的には下図・下表のような式となります。
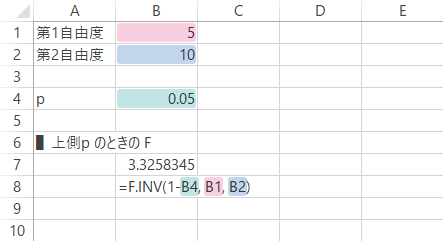
| B8 | =F.INV(1-B4, B1, B2) |
|---|
戻り値: 3.326。これは,下のグラフの横軸・ポインターが指示する点です。
Step 3下側確率p のときの F
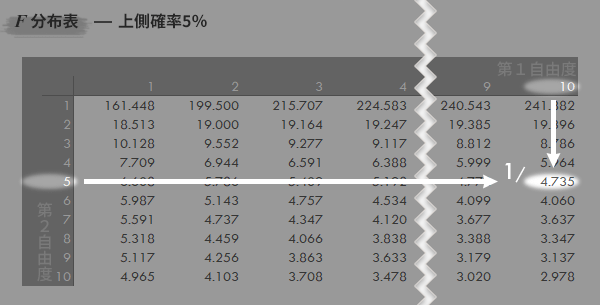
下側p=0.05のときFは,F分布表(上側)において 自由度を入れ替えたFの逆数で求められます(下図矢印の参照,=0.211)。
Step 4F.INV.RT, F.INV関数
こちらも上側と同様に,F.INV.RT関数で求めます。
この関数の引数が上側のpを要求する点に注意して式を組み立てると,具体的には下図・下表のようになります。

| B7 | =F.INV.RT(1-B4, B1, B2) |
|---|
またこれは,先と同様F.INV関数を利用して求めることも可能です。
この場合,式は下図・下表のとおりです。
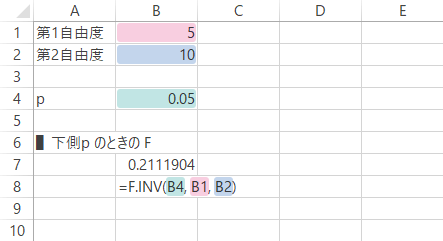
| B8 | =F.INV(B4, B1, B2) |
|---|
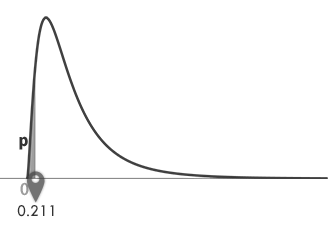
戻り値: 0.211。これは,下のグラフの横軸・ポインターが指示する点です。
Next
その他の参照
このサイトの関連How-toです。
- 正規分布の確率とパーセント点の計算
- 標準正規分布の確率とパーセント点の計算
- t分布の確率とパーセント点の計算
- χ2分布の確率とパーセント点の計算
- 母比率の信頼区間の推定
- 分布曲線のグラフ―確率とパーセント点のビジュアライゼーション
メインサイト「ひとりマーケティングのためのデータ分析」の分布に関連するHow-toです。