折れ線グラフを描いてみたはいいものの,系列多すぎ密度高すぎでグラフが読みにくい!――を解決する試み
Step 0はじめに
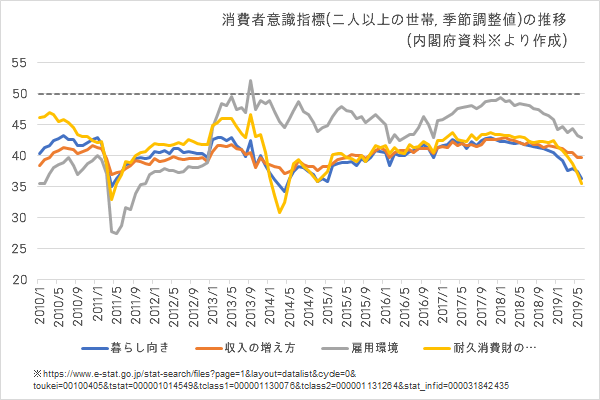
個別の具体的な数字はともかく,とりわけ値の多寡の移り変わるさま,すなわち推移に注視してみたいとき,折れ線グラフは下図のように十分な仕事を果たします。
ここでソースを下表に変えてみたいと思います。12指標24期にわたる架空のindex(t=0時点の値を1とした場合の換算値)です。
DL
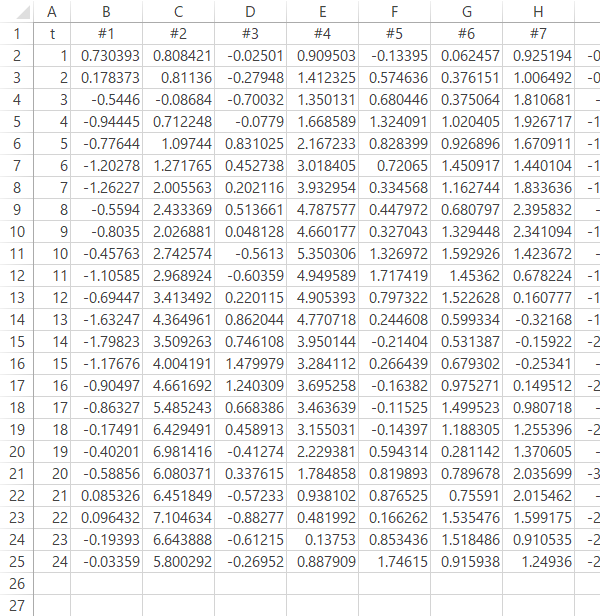
系列の数にして3倍にも至れば,先のような整然とした印象もさすがに維持はできません。こうした場合は層別ができればそれを経るのが定石でしょうが,ときに不可能であったり一連の塊を崩すのが不都合であったりといったケースも出てきます。
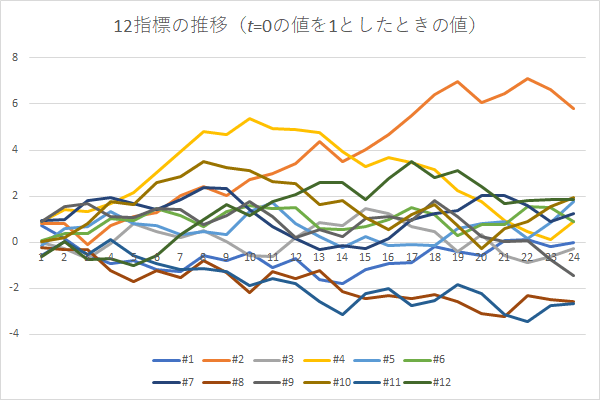
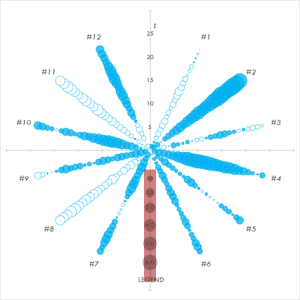
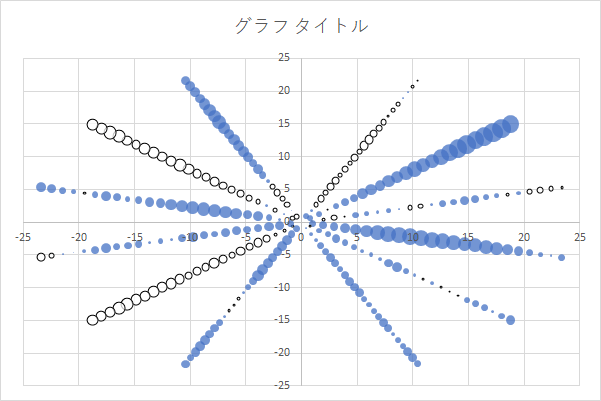
そうした状況下で,読みにくさを解決できないか試行するのがこの頁の趣旨となります。具体的には,下図のようなグラフで道筋を立てたいと思います。
このグラフは時間の経過を放射状に表現するので,多くの系列が混在しても破綻しにくく,円が大きさを与えられて連なることから盛衰をシンプルに理解できます。そうした単純さを優先する分,各ポイントでの値そのものの測りやすさを犠牲にしています(凡例に照らしてアバウトにしか分かりません)。
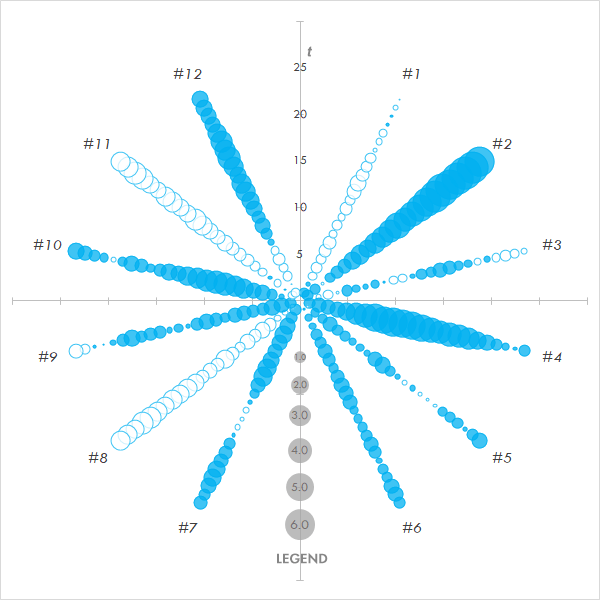
なお実のところ,この図に関してコンセンサスがありそうなところの名称を筆者は知りません。図的特徴からふだんは「スプラッシュチャート」と勝手に呼んでいます。
工程
Step 1
次の見出しを用意します。
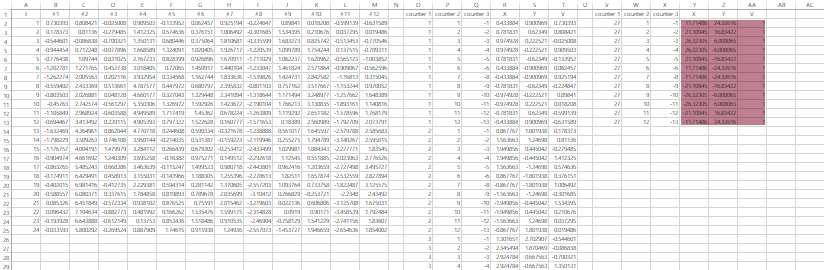
実際に作図に必要なものはX,Y,Vの3列で,counter 1-3はX,Y,Vを計算するための部品です。
Step 2
counter 1をつくります。変数の数をv,サイズをnとしたとき,
具体的には,同じ数字をv個ずつ繰り返しながら1~n(ここでは24)の連番を用意します。つまりこの作業で,12*24=288個のセルが埋まります。
| O2 | =CEILING.MATH((ROW()-1)/COUNTA($B$1:$M$1)) |
|---|
Step 3
counter 2をつくります。変数の数をv,サイズをnとしたとき,
具体的には,1~vの連番をn(ここでは24)セット用意します。この作業でも288個のセルが埋まります。
| P2 | =COUNTIF($O$2:O2,O2) |
|---|

Step 4
counter 3をつくります。変数の数をv,サイズをnとしたとき,
【vが偶数の場合】具体的には,-1~-(v+1)の負の連番をn(ここでは24)セット用意します。このとき,下段の図の赤色部分に要素が乗っかるのを防ぎたいので,v/2+1相当部分のカウントを1つ飛ばして埋めていきます。つまり,この例の場合は,-1,-2,-3,-4,-5,-6,-8,-9,-10,-11,-12,-13を繰り返します。
【vが奇数の場合】いろいろな対応が考えられますが,たとえば,0を始点に(v+2)/vずつ負方向へ下っていく負の連番をn(ここでは24)セット用意するなどします。たとえばv=5の場合,0,-1.4,-2.8,-4.2,-5.6といった具合でつくります。
Step 5
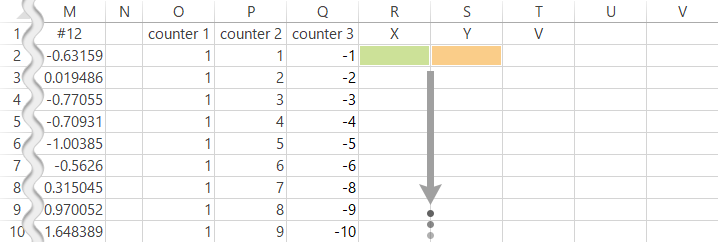
下式でX,Y座標をつくります。
| R2 | =O2*COS((2*PI()*Q2)/(COUNTA($B$1:$M$1)+2)+1/2*PI()) |
|---|---|
| S2 | =O2*SIN((2*PI()*Q2)/(COUNTA($B$1:$M$1)+2)+1/2*PI()) |
Step 6
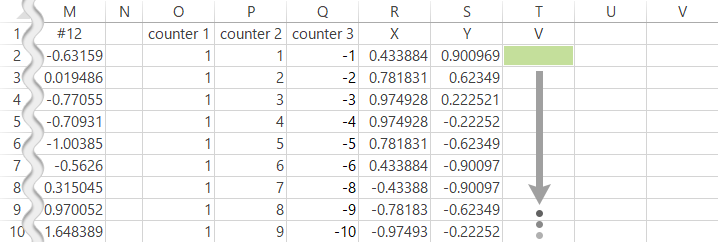
元表とcounter 1,2を突合します。
| T2 | =INDEX($B$2:$M$25, O2, P2) |
|---|
Step 7
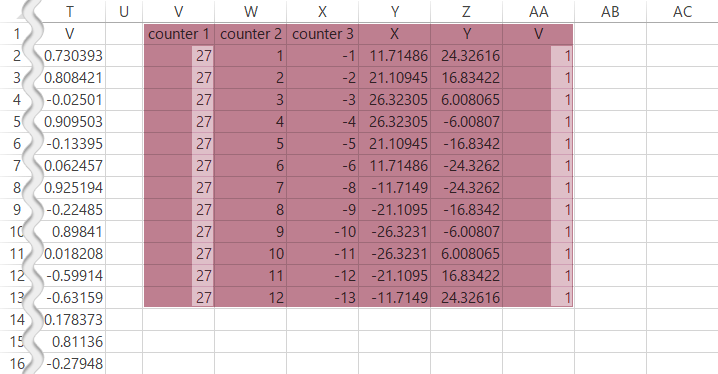
図に連なる円の束がどの変数のものかを示す,ラベル系列用のデータを別途つくります。基本的にはこれまでの作業の繰り返しですが,「counter 1」にはnよりも若干大きめの任意の値を,「V」には1を(どのみち不可視にするので0以外の値であれば何でも)指定しておけばOKです。
Step 8
下の図の強調部分を選択し,バブルチャートを挿入すると…
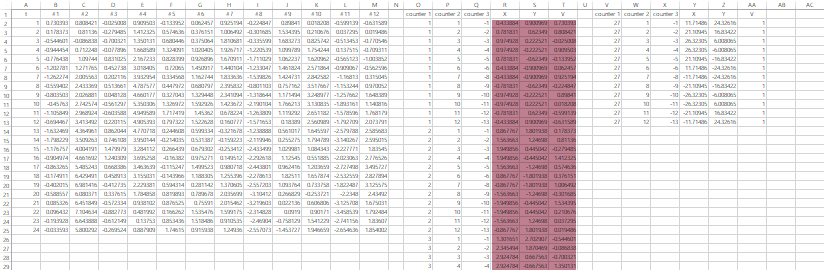
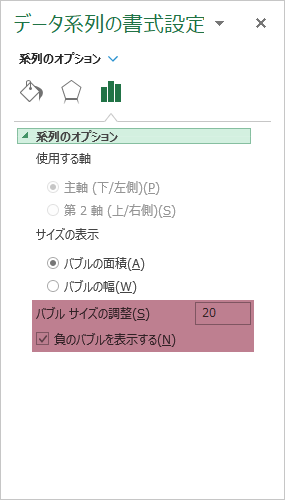
このようなグラフが描けます。デフォルトの状態では円の大きさが過剰で見にくくなったので,

「バブルサイズ」で円の視覚的なバランスを調整します。ついでに,この場合の元データは負の数も扱っているので「負のバブル」も表示できるよう設定します。
目的とするグラフをほぼ得ましたが,変数名は未だ付置していないので次にこれを対処します。
Step 9
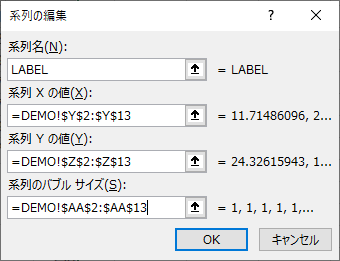
下の図の強調部分を選択し,あたらしい系列としてグラフに差し込みます。
この例の場合は,具体的には下のように処理します。
下の図にいうオレンジの点があたらしく挿入した系列です。これにラベルを表示させるようにして,
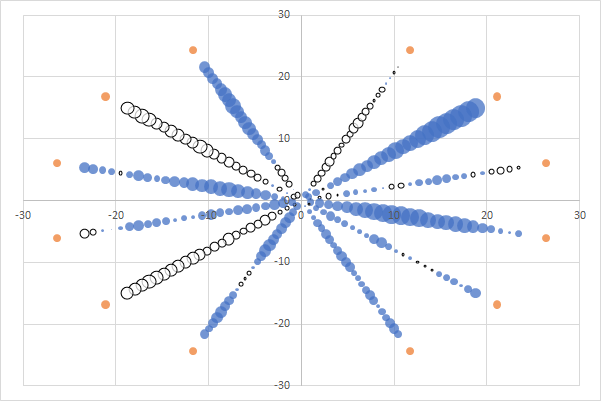
ラベルの内容を,下表の強調範囲とすれば…
こういった感じで変数名を表記できます。この系列の塗色(下の図にいうオレンジ色)は邪魔なので,「なし」にして飛ばしておきます。
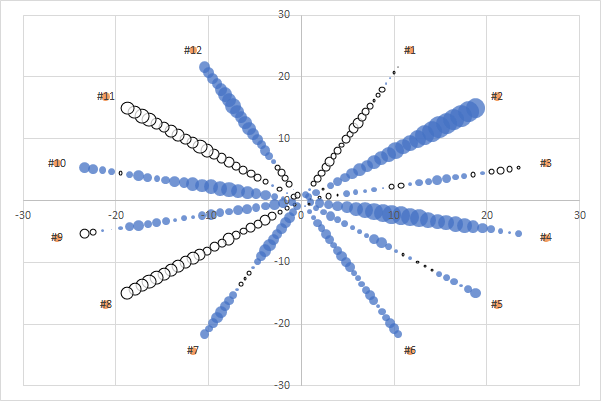
Step 10
凡例や目盛については,作図の趣旨を鑑みれば描画されるべき理由も薄いかもしれません。ここでは例としてあえて描画します。
具体的に,それらは先のラベルと同様に独立の系列で描画します。したがって次のようにデータを用意したうえで,あたらしい系列としてグラフに加えます。
そしてそれらにデータラベルを重ねてやれば,凡例や目盛の役割を担わせることができます。
Step 11
多変数の推移を知るための折れ線の代替表現,完成です。

その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の散布図に関するHow-toです。