等分散の検定(等分散性の検定, 母分散の比の検定) with Excel
Step 0シチュエーションの設定
都市型ホテルXは,直営のレストランで小規模な回転寿司コーナーを導入することになりました。これに関してXは,シャリ玉ロボットの導入を検討しています。現在のところ,やや安価な「マシンA」と,平均的な価格でメンテナンス性に利がある「マシンB」がその候補として検討されています。
いずれも,カタログスペックではXの要求する「(シャリの)量目15g」という基準を満たすことができます。ただ,カタログからは窺えない性能差が導入後に露見しても不都合ですので,Xは実機テストをおこなってみることにしました。下表がその結果です(単位グラム。無作為による抽出。なお,ここでは諸々の制限からデータの数は均一にできなかったと仮定します。また均一であったとしても手続きは変わりません)。
DL
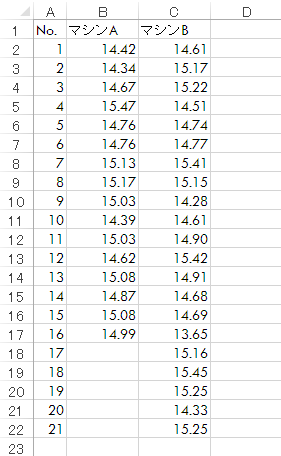
平均を求めてみると,両者に大きな差は見られません(下表。小数点第3位で四捨五入)。また,カタログスペック(量目15g)から大きくかい離した性能でもなさそうです。
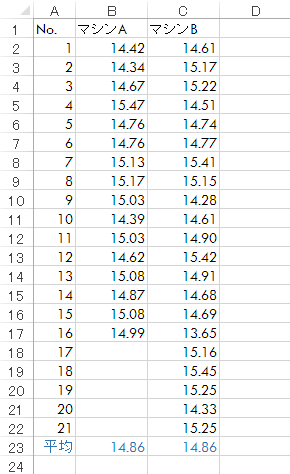
では,カタログに表記のない分散(不偏分散)はどうでしょうか。次のように計算してみると
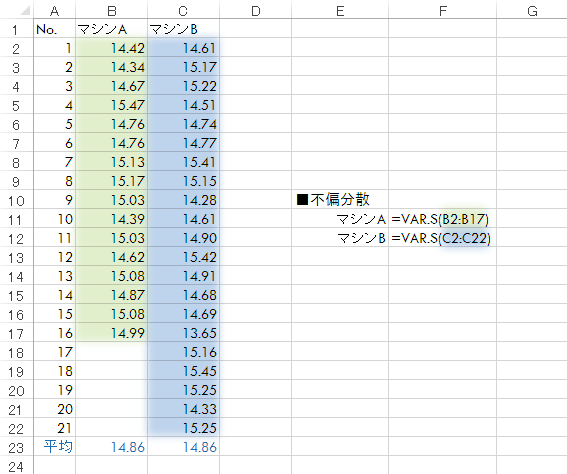
順に0.1,0.2と異なる値が見られました(標準偏差にすると順に0.32g,0.45g)。
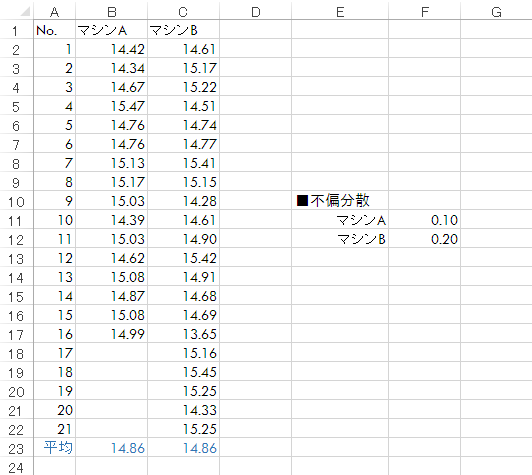
この差が確率的に意味のあるものなのか,以下F検定によって確認します(両側検定, 有意水準5%)。
工程
Step 1前提
仕様表から,母集団は正規分布にしたがうものとみなします(仮定)。また,帰無仮説H0と対立仮説H1は次のように設定します。
| H0 | σ2A=σ2B(マシンA・Bによる量目の母分散に差はない) |
|---|---|
| H1 | σ2A≠σ2B(マシンA・Bによる量目の母分散に差がある) |
ただし,σ2:母分散。
Step 2見出しの入力
検定統計量(T)は次の式によって求められます。分散の値の大小によって上下いずれかの式を利用します。この方法は(Excelを使わなくても)上側確率で示されるF分布表を利用できる点において利があります。
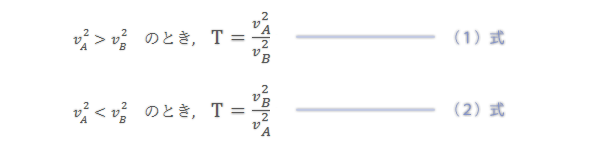
ただし,v2A: A群の不偏分散, v2B: B群の不偏分散。
これをシート上で計算するため,下表のような見出しを作成しておきます。
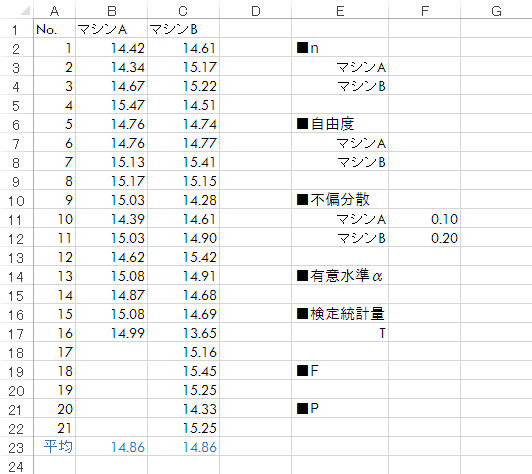
Step 3n, 自由度 の入力または計算
A群・B群についてn(サンプルサイズ)を入力します。これをもとに自由度(n-1)を求めます。
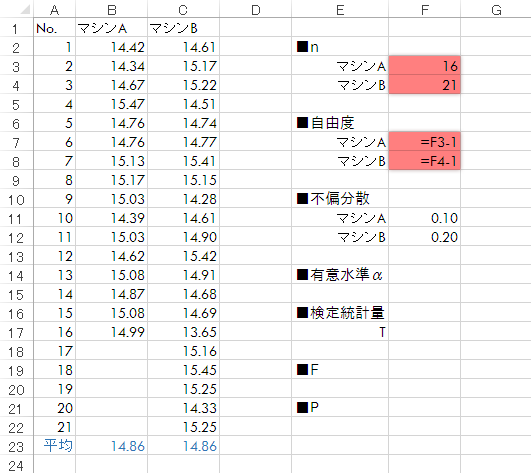
Step 4有意水準の決定
有意水準を指定します。ここでは設定のとおり0.05(5%)と入力します。
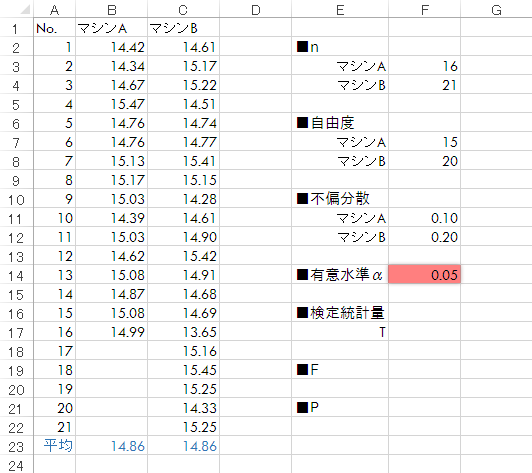
Step 5検定統計量(分散の比)の計算
Tを求めます。
v2A<v2Bより,この例ではstep2-(2)式でTを求めます。
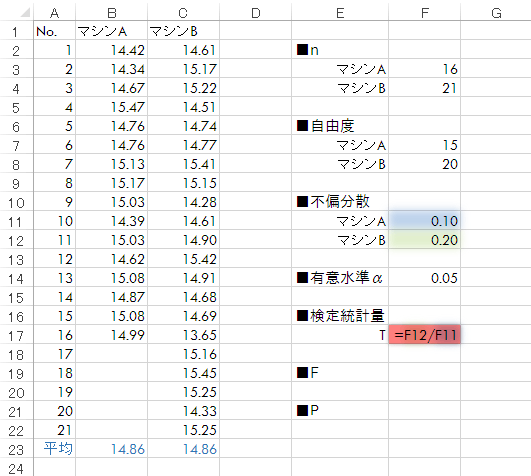
Tは2.03となりました。

これ以降の手続きは,
- 棄却限界値による判断 Step6
- P値による判断 Step7
と分岐します(任意に選択。迷えばStep7)。
[分岐]Step 6棄却限界値の計算と仮説の判断
棄却限界値を求めます。
Step2-(1)式を用いる場合(つまりv2A>v2Bの場合),自由度は
| 第1自由度 | セルF7(マシンA群の自由度) |
|---|---|
| 第2自由度 | セルF8(マシンB群の自由度) |
とし,同様にStep2-(2)式を用いる場合(つまりv2A<v2Bの場合),自由度は
| 第1自由度 | セルF8(マシンB群の自由度) |
|---|---|
| 第2自由度 | セルF7(マシンA群の自由度) |
として棄却限界値を求めます。両側検定ですので,式の構造は
| F | =F.INV.RT(α/2, 第1自由度, 第2自由度) |
|---|
となります。この事例は(2)式を利用するケースですので,具体的な式は下表のようになります。

結果,2.76であることがわかりました。

先のステップで求めた検定統計量の値とともに,この値をF分布のグラフ(第1自由度20, 第2自由度15)にプロットしてみると下図のようになります。T<Fとなり棄却域にかからないので,帰無仮説は棄却できません(意味のある差を主張するには証拠不足)。
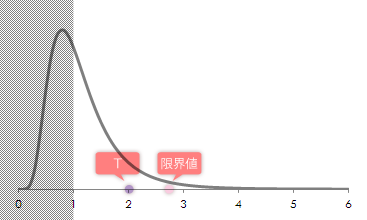
[分岐]Step 7P値の計算と仮説の判断
P値を求めます。
Step2-(1)式を用いる場合(つまりv2A>v2Bの場合),自由度は
| 第1自由度 | セルF7(マシンA群の自由度) |
|---|---|
| 第2自由度 | セルF8(マシンB群の自由度) |
とし,同様にStep2-(2)式を用いる場合(つまりv2A<v2Bの場合),自由度は
| 第1自由度 | セルF8(マシンB群の自由度) |
|---|---|
| 第2自由度 | セルF7(マシンA群の自由度) |
としてP値を求めます。両側検定ですので,式の構造は
| P | =2*F.DIST.RT(T, 第1自由度, 第2自由度) |
|---|
となります(上側P値の2倍)。この事例は(2)式を利用するケースですので,具体的な式は下表のようになります。
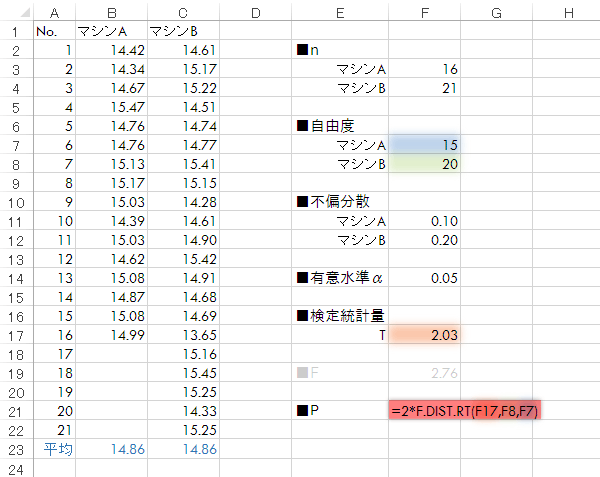
なお,ここでの例のようにシートに元データを列挙している場合(紫の囲みの部分),F.Test関数によって分散の大小を気にすることなく,ダイレクトにP値を求めることもできます(下図)。
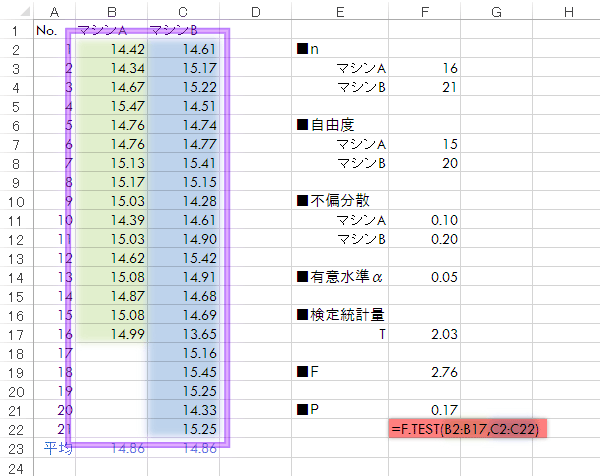
結果,0.17であることがわかりました。

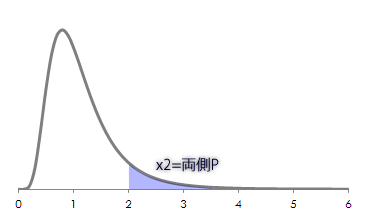
この値はF分布のグラフ(第1自由度20, 第2自由度15)に以下の領域で示されます。P>αとなり,帰無仮説は棄却できません(意味のある差を主張するには証拠不足)。
Step 8X社の判断
都市型ホテルXは,マシンA・Bの分散に有意な差は見られなかった(≒性能差があると大きな声で言えない)と判断し,価格とメンテナンス性に焦点を絞って検討をつづけることを決めました。
参考にした書籍
- 菅 民郎(2013)『Excelで学ぶ統計解析入門 Excel2013/2010対応版』オーム社, pp.154-155.
- アミール D. アクゼル・ジャヤベル ソウンデルパンディアン(2007)『ビジネス統計学[上]』鈴木一功監訳, 手嶋宣之・原 郁・原田喜美枝訳, ダイヤモンド社, pp.404-411.
- 上田拓治(2009)『44の例題で学ぶ統計的検定と推定の解き方』オーム社, pp.88-89.
等分散の検定に対応するExcelアドインソフト
- エクセル統計 BellCurve
- 「2標本の比較」「等分散性の検定」(信頼区間・検出力も出力)
- Statcel4(4Stepsエクセル統計)
- 「母分散の比の検定と推定」(信頼区間に対応。棄却限界値も出力してくれるのが地味に便利)
その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の有意性検定に関するHow-toです。