移動平均法による季節調整 with Excel
Step 0シチュエーションの設定
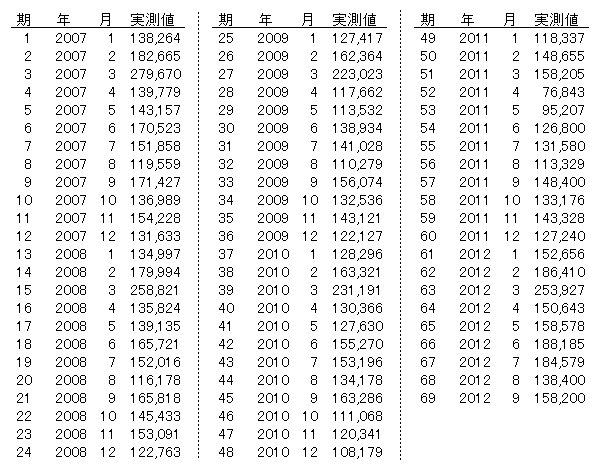
2007年1月から2012年9月の6年弱にわたる月次の軽自動車販売台数のデータです。感覚的に,これは季節性や無作為性を強く含むであろうデータのように思われます。このデータを用いて,移動平均による季節調整をおこない,トレンドを確認します。
[データの出所: 日本自動車販売協会連合会ウェブサイト ―url: http://www.jada.or.jp/contents/data/index09.html; リンク切れ]
アウトライン
Step 1
ここでは,引用した時系列データを次のように考えます。
- ある期における実測値は,当該期における季節性・トレンド性・循環性・無作為性の関数であるとする。

Step 2
- これらの要素は,実際には乗法モデルにしたがう関係にあるとする。
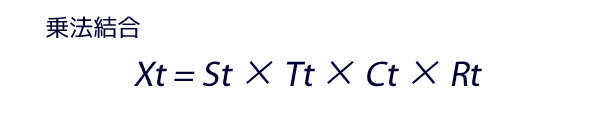
Step 3
以下,ここでおこなう季節調整のStepです。
前段はt期の実測値(Xt)から季節性(St)を取り除き季節調整済みの実測値を導くことを,後段は季節調整済みの実測値から無作為性(R)を取り除き,トレンド循環値(T×C)を導くことを目的とします。
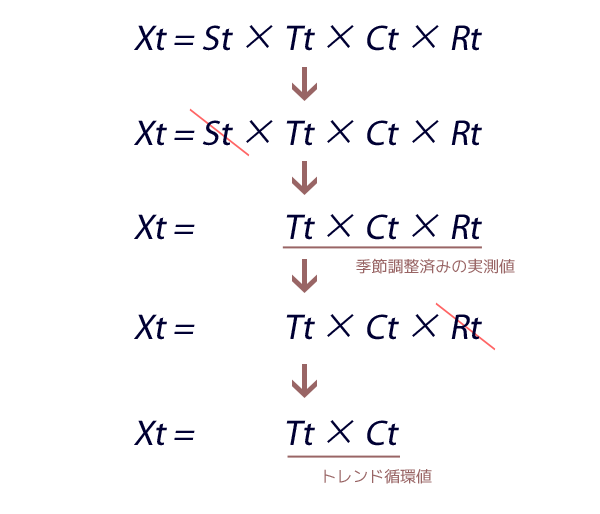
工程
季節調整済み実測値の計算
Step 4非中心化移動平均の計算
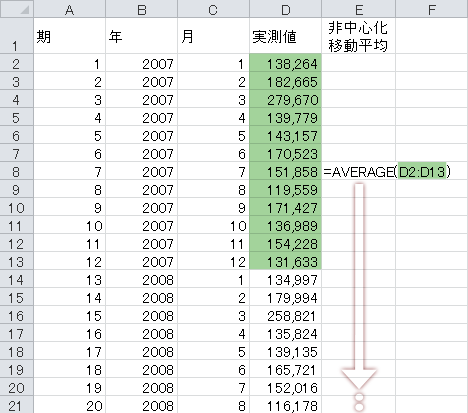
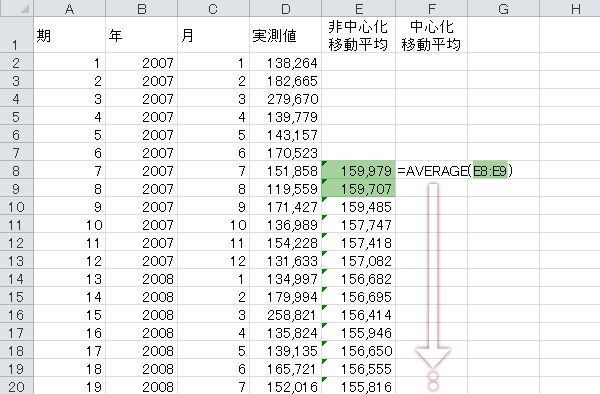
12ヵ月中心化移動平均を計算するための準備です。7期目から上に7期,下に6期(いずれも当該行を含む)の移動平均を計算します。
次に,この計算式を表の最下行から数えて6期目(12期分のスパンをとることのできる下限)までコピーします。
[よりみち] 移動平均,中心化なんて面倒だし後方でとればいいじゃん?
Step 5中心化移動平均の計算
12ヵ月中心化移動平均を計算します。非中心化移動平均2期分の平均を求めます。
次に,この計算式を表の最下行から数えて7期目(2期分のスパンをとることのできる下限)までコピーします。
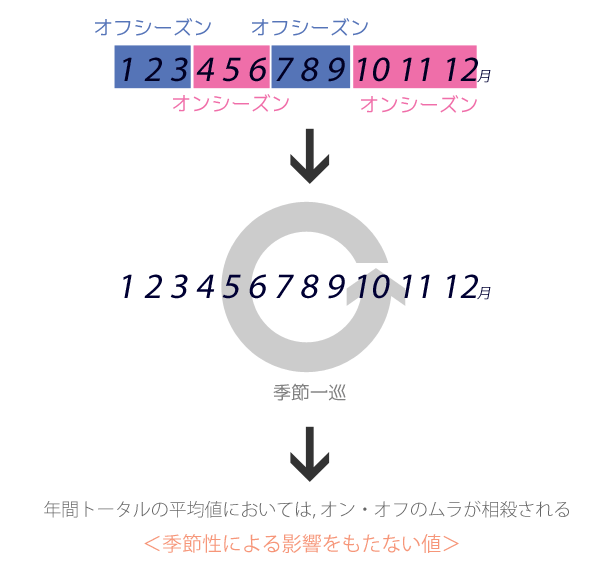
Step 4およびStep 5で移動平均(MA)をとる理由の1として,季節性をとりのぞくことがあります。たとえば下図のように,年間を通じてオンシーズン・オフシーズンが見られるような環境下では,各月の値が良かったのか悪かったのか,単純比較は難しいところです。
しかし,季節が一巡する年間のスパンで平均や合計をとることによって,結果的にはオン・オフのムラは相殺される方向に力がはたらきます(データの平滑化)。
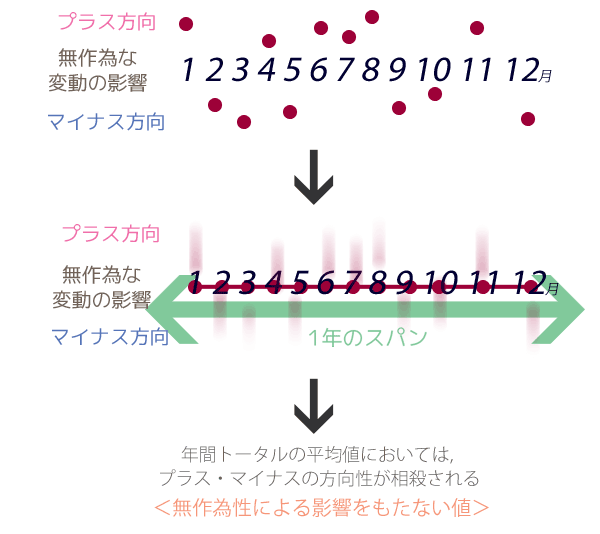
いまひとつの理由として,無作為性をとりのぞくことがあります。これが排除される理由も,季節性と同じです。
以上から,移動平均は,季節性と無作為性がとりのぞかれた値とみることができます。つまり,移動平均(MA)は 次式であらわすことができます(MA=T×C)。
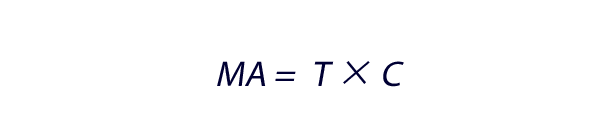
Step 6比の計算
実測値を中心化移動平均で除し,比を計算します。
次に,この計算式を左の「中心化移動平均」列の最下行までコピーします。
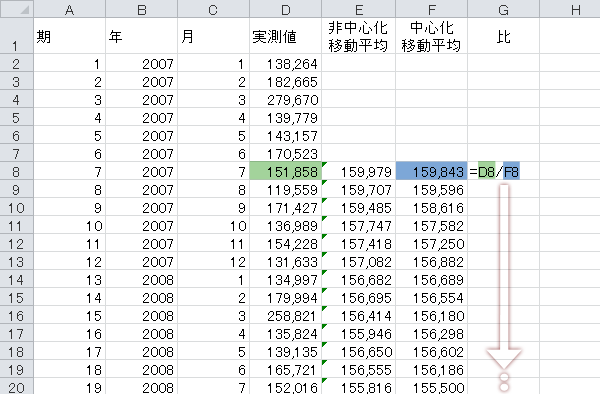
実測値をXとしたとき,この比は上のようにX/MAであらわせます。このX/MA式に,先の乗法モデルの式,および移動平均の式を代入し変形すると,下のように表せます。つまり,この比が意味するものは無作為性を含む季節値(S×R)です。
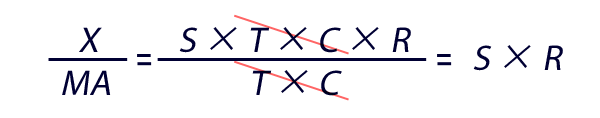
Step 7季節指数の計算(1)
ということで,これ(S×R)より無作為性(R)を除去して季節指数(S)を求めます。
単純な季節指数は,下の計算式で求められます。
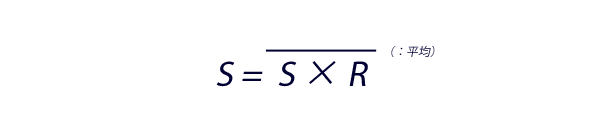
この頁の例のもと,上記の式を利用した場合には,最長5年の「比」の平均を求め,季節指数を導くことになります(一般的な季節調整の手続き)。以下,しばらくそのための作業が続きます。
だだし平均とはいえ,この例では単純平均を選択することは避けたいと思います。代わりにトリム平均(データ群からMIN・MAXを除外した上で求める平均)を使いたいと思いますが※,この理由は,当該期間のデータを使う場合は季節性を著しく振れさせるおそれのある“異常事態”の影響力を調整した方がbetterかと考えたゆえです。いずれの平均を用いるべきかはケースバイケースで判断してください。
※ したがってこのケースの場合,正確には最長“3年”の平均となります。
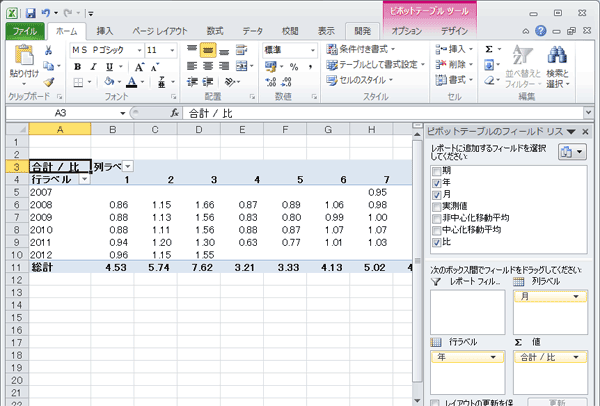
では,手順に戻ります。ピボットテーブルを使って,年別月別の比のクロス表を作成します(ここでは別シートに作成しました)。
Step 8季節指数の計算(2)
このクロス表をもとに,月ごとの「比」のMIN・MAXを12ヵ月分求めます。
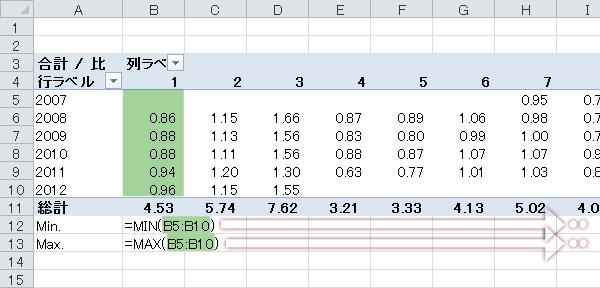
Step 9季節指数の計算(3)
上で求めたMIN・MAXを除いた,「比」のトリム平均を計算します(ここではセルB14)。
入力した計算式を残り11ヵ月分コピーします。
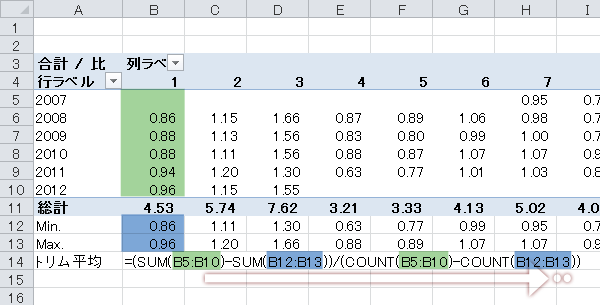
Step 10季節指数の計算(4)
1月~12月のトリム平均を合計します。ここではおよそ11.95になりました。
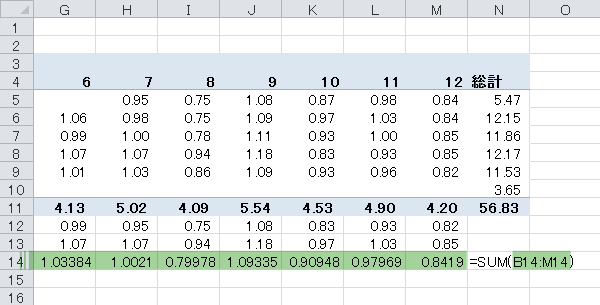
Step 11季節指数の計算(5)
このトリム平均の合計が,ちょうど12となるよう補正します(12ヵ月分の指数ゆえ)。下のように,「12」を「12ヵ月分のトリム平均の合計値(ここでは11.95)」で除したものを,1月のトリム平均に乗じます。
入力した計算式を残り11ヵ月分コピーします。
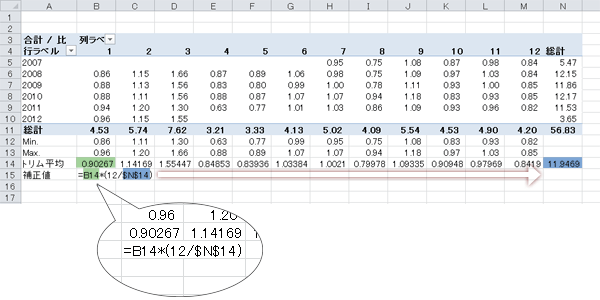
Step 12季節指数の計算(6)
念のため,補正した1月~12月のトリム平均を合計し検算してみます。
この値が12になることを確認しておきます。
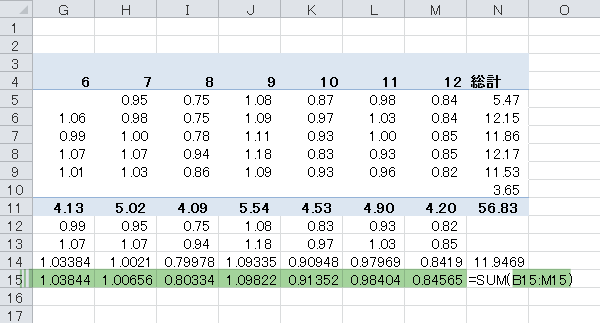
Step 13季節指数の計算(7)
前の手順までに求めたトリム平均の補正値をコピーし,「季節指数」として元の表に行列を入れ替えて貼り付けます。
12ヵ月分のデータを表の最下行まで繰り返し貼り付けていきます。
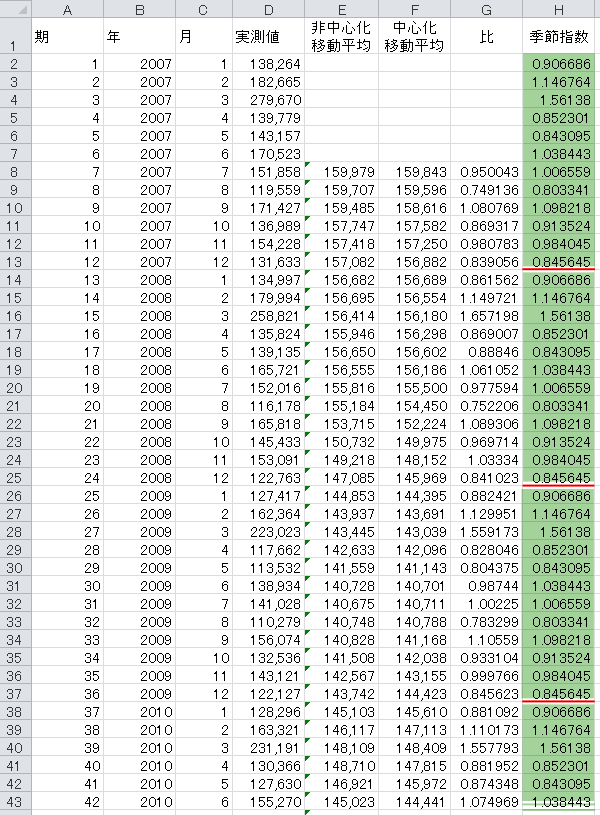
Step 14季節調整済実測値の計算
季節指数をもとに実測値を補正します。「季節調整済の実測値」列の計算式は下図のとおりです。
次に,この計算式を表の最下行までコピーします。
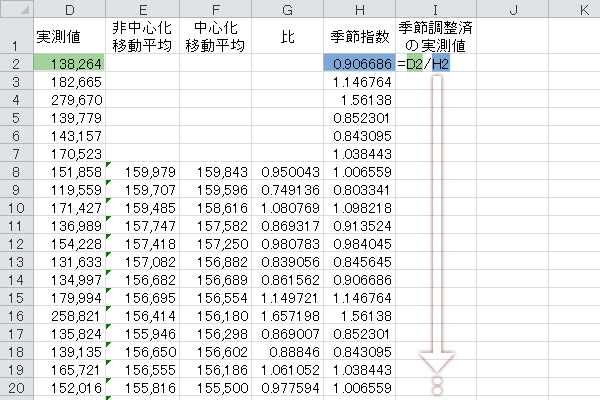
ここで上の「季節調整済の実測値」X/Sに,先に示した乗法モデルの式を代入すると,下のように変形できます。この「季節調整済の実測値」T×C×Rは季節性が取り除かれた値であることがわかります。
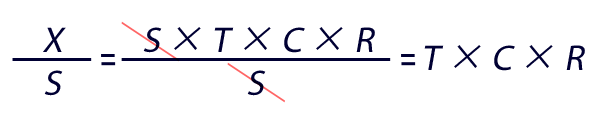
季節調整をおこなう場合,一般的にはこのT×C×Rを求めることが目的とされます。しかし,せっかくここまで面倒な計算を済ませたのなら,トレンド性(T)と循環性(C)からなる,純然な(?)パターンを確認しておいても損はないと思います(トレンド分析)。具体的には,このT×C×Rよりさらに無作為性(R)を排除することを狙いとします。つまり,ここで再び移動平均を利用します。
以下,その手続きです。
トレンド循環値の計算(季節調整済み実測値から無作為性をとりのぞく)
Step 153期移動平均の計算
T×Cを把握するため,計算した季節調整済の実測値をもとに12ヵ月中心化移動平均を求めると,前後に6期づつの欠落が生じてしまいます。トレンドの確認という観点に重きを置く場合には,同じ欠落でも後方のそれはできれば避けたいところです(過去の動向より直近の動向がもつ情報の重要性)。
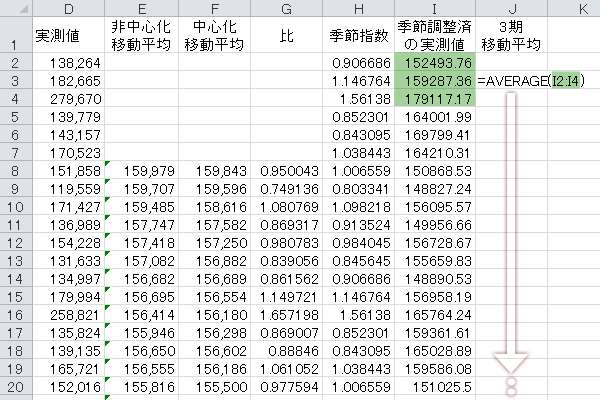
そこで12ヵ月中心化移動平均でなく,「3×3期移動平均」という“移動平均の移動平均”で代用することとします[マクリダキス, フィールライト(1995)]。その手続きの1として,ここではまず「3期移動平均」列を計算します。計算式は下図のとおりです。
次に,この計算式を表の最下行から1行手前の行(3期分のスパンをとることのできる下限)までコピーします。
Step 163x3期移動平均の計算
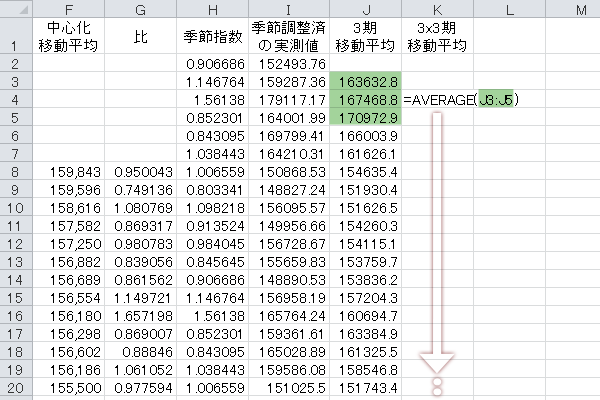
手続きの2として,計算した3期移動平均をもとに3×3期移動平均を計算します。「3×3期移動平均」列の計算式は下図のとおりです。
次に,この計算式を表の最下行から2行手前の行(3期分のスパンをとることのできる下限)までコピーします。
Step 17欠落データの対策(1)
3×3期移動平均でも直近2期には対応できません。先のように,トレンド分析の観点からは直近の情報の欠落は避けたいところです。したがってあくまで姑息的ですが,欠落部分を埋める工夫を施します[前掲書]。
まず,2期前の「3×3期移動平均」の値については,下図のように「季節調整済の実測値」の3期移動平均にて代用します。
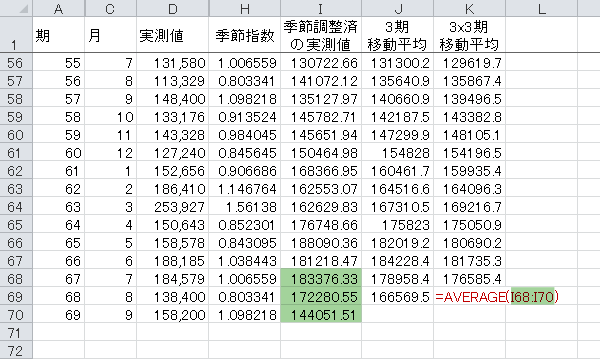
Step 18欠落データの対策(2)
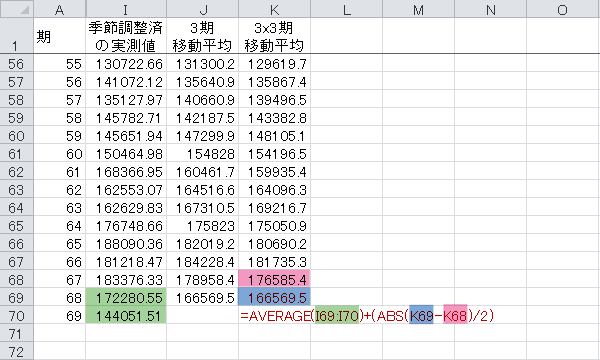
1期前については,「季節調整済の実測値」の2期移動平均にて代用することとします。しかし2期分のものですので,この値のままでは,ここで言う68期と69期の中間(言うなれば68.5期)のものとなってしまいます。そこで補正を加えます。
補正については,直近2期の「3×3期移動平均」の差を2で除した値を適用するものとします。つまり,直近の「3×3期移動平均」移動平均から0.5期分に相当する値を加え,代用値として利用します。
Step 19グラフ化
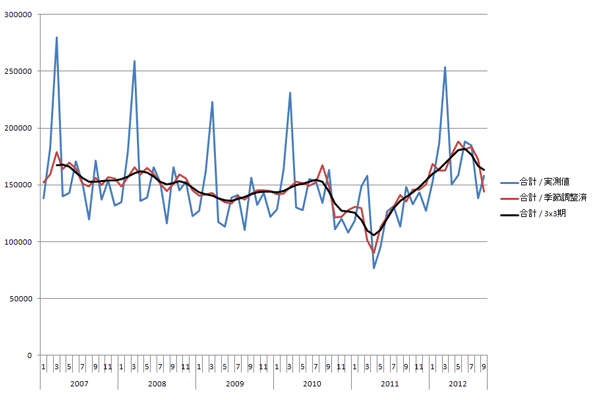
最後に,「実測値」「季節調整済の実測値」「3×3期移動平均」の3列をソースに線グラフで可視化すると,下のようになります(ここではピボットグラフを使用しています)。黒い線がトレンド循環値(T×C)です。この線を見る限り,2010年中盤から波の振れが従前と比べて大きくなっている様子がうかがえます。
Step 20追記(2013.6)
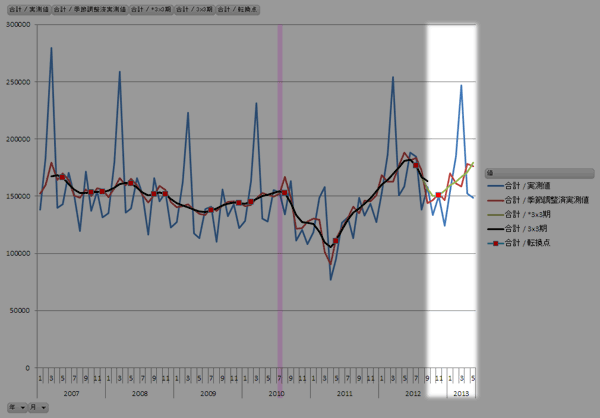
季節指数を所与のものとして,その後のデータを加えてみます。あらたに求めたトレンド循環値は,下のハイライト部分に薄い緑の線で示しています。また,赤いマーカーは3x3移動平均線の転換点です。
参考にした書籍
- スピーロス マクリダキス・スティーブン C フィールライト(1995)『計画策定と意思決定のための予測手法入門』加藤五郎訳, 同友館, pp.81-101.
時系列分析ができるExcelアドインソフト
- エクセル統計 BellCurve
- 「時系列分析・曲線のあてはめ」各手法(期別平均法・連環比率法・EPA法などが利用可能)
その他の参照
このサイトの関連How-toです。
メインサイト「ひとりマーケティングのためのデータ分析」の予測ツールに関するHow-toです。
同じくトレンド分析ツールに関するHow-toです。