BDAstyle

Business Data Analysis & Visualization with Excel

等確率楕円を重ねた散布図の作成 with Excel

はじめに

  • 下記の手続きによる楕円は，nが小さいとき「R」・carパッケージのdataEllipse関数により出力される楕円より若干小さくなります。下記の内容を追う場合は，筆者がこのあたりの背景を記事の公開時点で消化できていないことをご承知の上でご利用ください。したがって厳密さが何よりも重要な場合には，「R」などの可視化手段が利用できる環境であればそちらで処理されることをおすすめします。

Step 0シチュエーションの設定

ここでは，リサーチサービス社の取引履歴から起こした次のデータをもとに例示します(2変数)。

DL

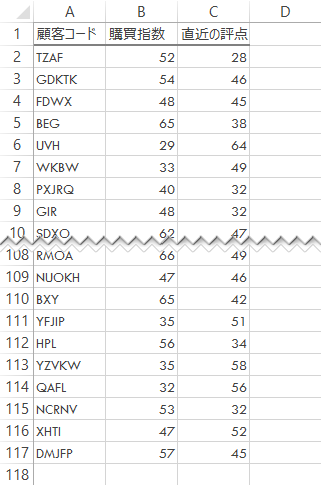
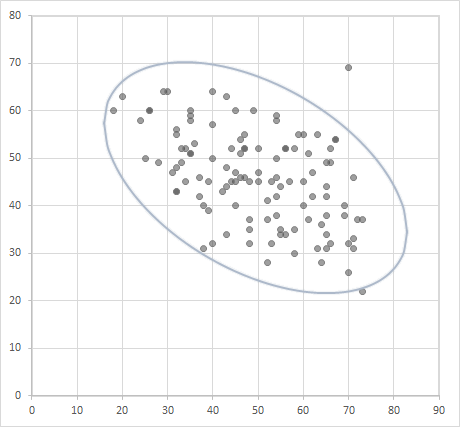
目的のアウトプットは下図のとおりです。「等確率楕円」「信頼楕円」「集中楕円」といった呼称があてられる確率楕円を，散布図に重ねます(α=5%)。

作図にあたり参考にした書籍およびPDF文書


工程

Step 1

まずは2変数をもとに予め散布図を作成し，これらの関係を概察しておきたいと思います。

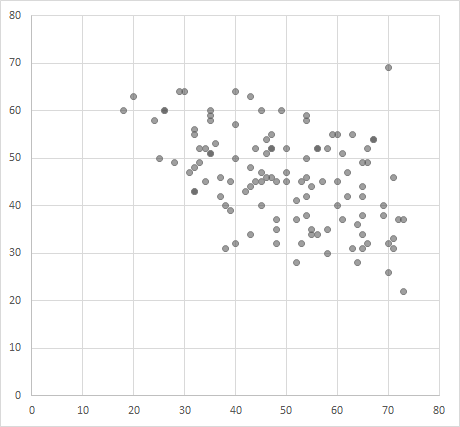
図からは，中強度の負の相関が目算できます。

ということを頭の片隅に置いたまま次の段階に移り元のデータ表の右方に下図のような見出しを用意します。

なお，これらは具体的に

  • n ―データ対の数
  • r ―相関係数(ピアソンの積率相関係数)
  • χ2(p,2) ―自由度2のカイ2乗分布における上側確率pのときのパーセント点
  • xl ―楕円のx軸に関する左端(min[x])
  • xu ―楕円のx軸に関する右端(max[x])

を指します。

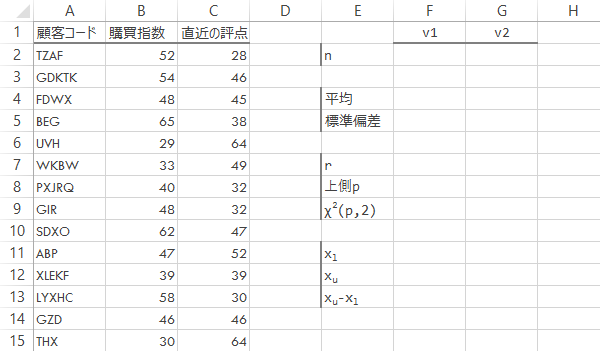
下図の彩色されたセルに，対応する下表の数式を入力し，データ対の数の他，2変数の平均・標準偏差を求めます。

F2 =COUNT(B:B)
F4 =AVERAGE(B:B)
G4 =AVERAGE(C:C)
F5 =STDEV.S(B:B)
G5 =STDEV.S(C:C)

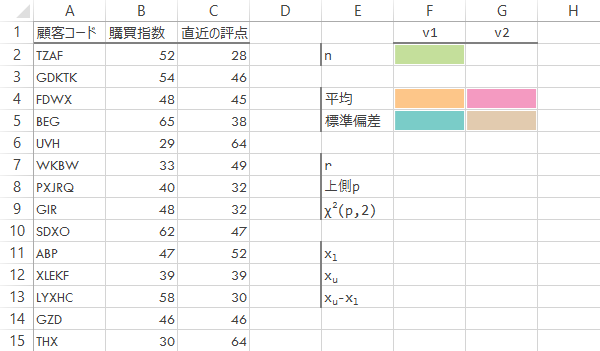
相関係数を求めます。

つづいて「上側p」には必要とする値を入力し(たとえば，95％等確率楕円が目的の場合p=1-0.95=0.05)，「χ2(p,2)」ではそれに対応するχ2値を求めます(後述のD2の分布は，自由度2のカイ2乗分布に近似する)。

F7 =PEARSON(B:B, C:C)
F8 0.05
F9 =CHISQ.INV.RT(F8, 2)

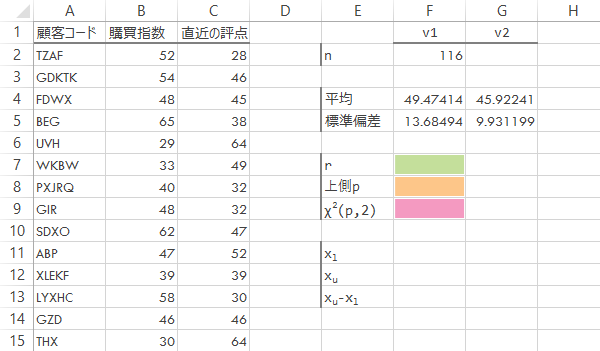
等確率楕円のx軸上での描画範囲を求めます (x̄-sxχ, x̄+sxχ) [s: 標準偏差]。

ただし，後述のyiを求める過程で元データによっては演算時にエラーが出てしまう(平方根の中で微小な誤差が生ずることに起因するもの)ので，ここではエラーをできるだけ回避させることを優先にし，若干の微小値を加減した上での丸め処理を重ねています。

F11 =ROUND((F4-F5*SQRT(F9))+0.00001, 5)
F12 =ROUND((F4+F5*SQRT(F9))-0.00001, 5)
F13 =F12-F11

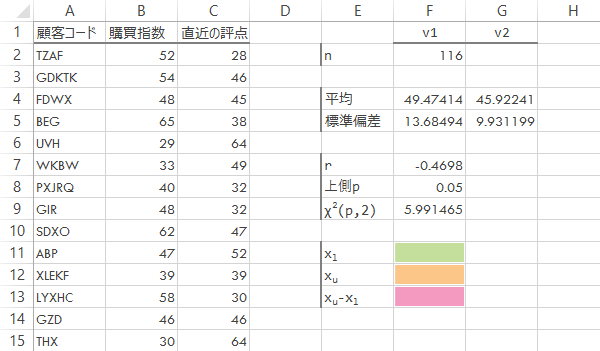
Step 2

このstepではデータ対のすべてに対し，マハラノビス距離(cf. 判別分析(マハラノビス)―"静岡理工科大学総合情報学部コンピュータシステム学科・知能インタラクション研究室")の2乗(D2)を求め，等確率楕円によって域外に区分される項目を探します。探索の必要がない(楕円を描くことだけが目的)場合は，Step 2, 3を飛ばして4へ飛んでもかまいません。

この場合，シートのさらに右方に下図のような見出しを用意しておきます。

2変数を標準化したとき，D2は下式によって求められます。

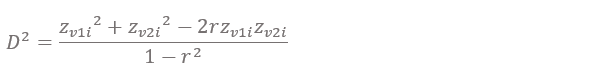
D^2=(〖z_v1i〗^2+〖z_v2i〗^2-2rz_v1i z_v2i)/(1-r^2 )

したがって，最初に2変数を標準化します(見出し直下に式を入力しn-1行分コピー)。

I2 =STANDARDIZE(B2, $F$4, $F$5)
J2 =STANDARDIZE(C2, $G$4, $G$5)

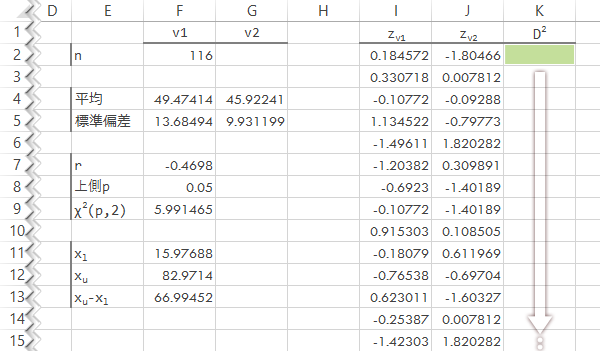
zv1, zv2をもとにD2を求めます(見出し直下に式を入力しn-1行分コピー)。

K2 =(I2^2+J2^2-2*$F$7*I2*J2)/(1-$F$7^2)

Step 3

項目の 域内｜域外 を判別します。これとχ2(p,2)を各個比較し，D2＞χ2(p,2)ならば当該項目を域外とします。

シート上での判別の方法はいろいろあるかとは思いますが，たとえば条件付き書式を利用し下図のような設定を元のデータ表に施すと

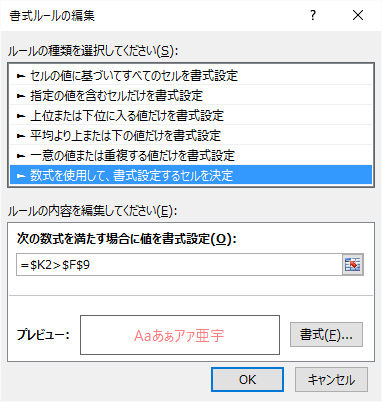
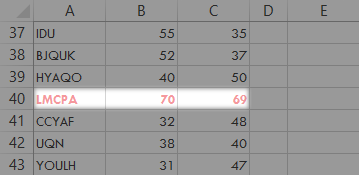
顧客コード「LMCPA」他が域外となることが書式によって自動的に強調されます。

Step 4

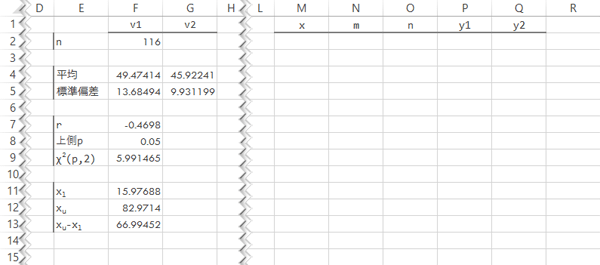
このstepでは楕円の(描画を目的として)座標を求めます。準備として，シートの右方に下図のような見出しを作成します。

なお，これらは具体的に

  • x ―x座標
  • m, n ―後述
  • y1 ―楕円の上半円についてのy座標
  • y2 ―楕円の下半円についてのy座標

を指します。つまり楕円は上下2系列に分けて描画します。

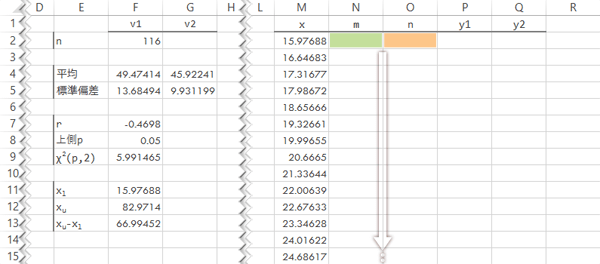
xの初期値，およびそれに範囲(xu-xl)の1/100を加えて次のx値を作ります。要するに区間の幅をレンジの1/100としてデータポイントを刻んでいくわけですが，1/100という数字には特段の意味があるわけではありません。後の工程で平滑線を描くことを考えると，だいたいこれくらいのデータポイントがあれば十分そうといったあいまいな判断からです。

なおここに言うセルM3の数式は，下方に100-1=99行分コピーします。このとき最下行のセルの値が，同じくここに言うセルF12の値と一致することになります。

M2 =F11
M3 =M2+$F$13/100

y1, y2は下式によって求めます。

y_i=(v2) ̅+s_v2 [r (x_i-(v1) ̅)/s_v1 ±√((r (x_i-(v1) ̅)/s_v1 )^2-{((x_i-(v1) ̅)/s_v1 )^2-χ^2 (1-r^2 )} )]

シート上でこのまま上式を組み立てるのはいささかの躊躇を覚えるので，ここでは先に式中の彩色箇所から別途計算していきたいと思います。具体的には，パープルの式をm，ブルーの式をnとして作業列上で処理します(入力後最下行までコピー)。

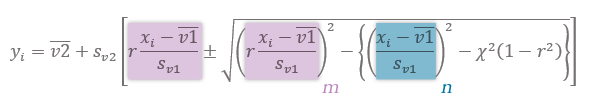
N2 =$F$7*((M2-$F$4)/$F$5)
O2 =(M2-$F$4)/$F$5

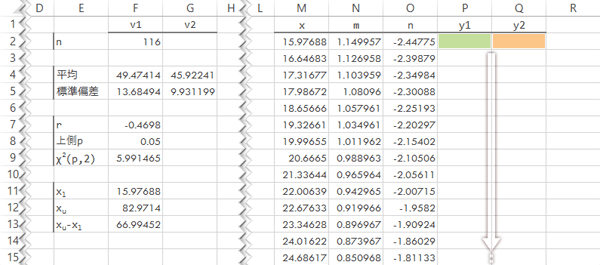
m, nを利用して先の式をy1, y2ともに組み立てます(入力後最下行までコピー)。

P2 =$G$4+$G$5*(N2+SQRT(N2^2-(O2^2-$F$9*(1-$F$7^2))))
Q2 =$G$4+$G$5*(N2-SQRT(N2^2-(O2^2-$F$9*(1-$F$7^2))))

Step 5

グラフ(先に作成しておいた散布図)をアクティブにして系列を追加します。

具体的にはx, y1の組み合わせが1つ，x, y2の組み合わせが1つの計2系列を組み込みます。

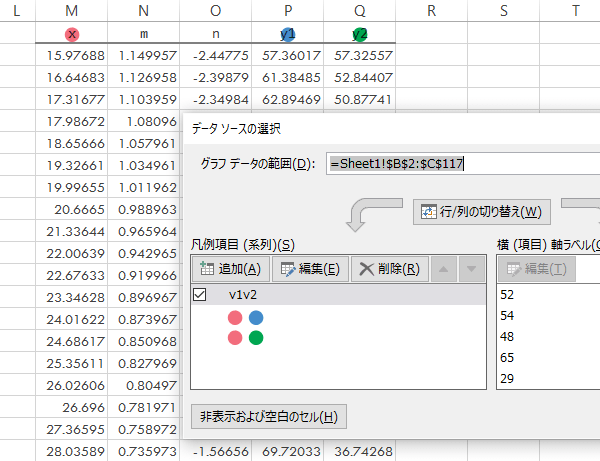
これにより，グラフは下図のような状態となります。

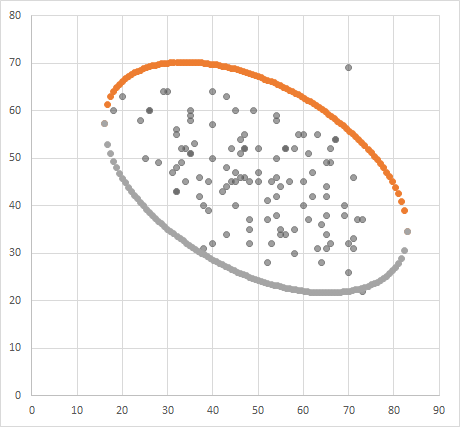
あたらしく追加した2系列の「グラフの種類」に関して，それぞれ「散布図(平滑線)」に変更します。

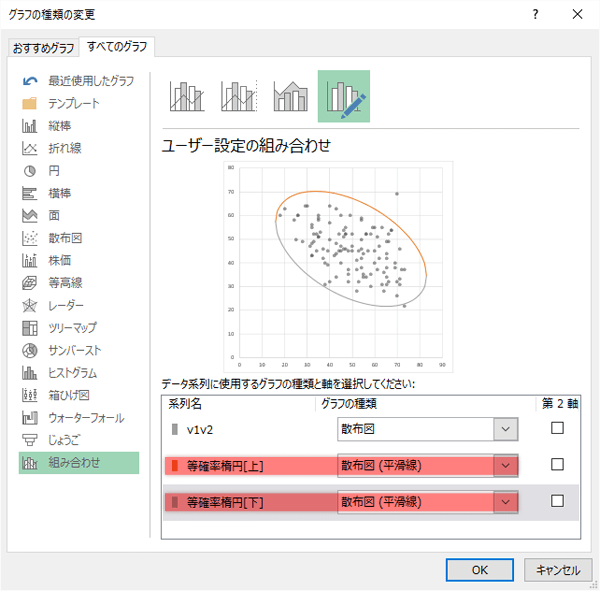
Step 6

平滑線の線色を任意のもので統一し，散布図に対する等確率楕円の重ね描きの完了です。

その他の参照