正規分布の確率とパーセント点の計算 with Excel
ショートカット
正規分布
Step 0シチュエーションの設定
ある建設資材製造会社が製造する直径50mm規格の丸鋼Aの製品品質は,平均 50.02mm,標準偏差0.07mmの正規分布にしたがうことがわかっています。
以下,この丸鋼Aの直径の計測値をxであらわします。
x から 確率p を求める
Step 1NORM.DIST関数
正規分布における下側確率(「累積確率」とも)は,ExcelではNORM.DIST関数で求められます。このとき,引数は次のとおりです。
- NORM.DIST(x, 平均, 標準偏差, 関数形式) ―"Office"
引数「関数形式」は,[true]の指定で下側(累積)確率が,[false]の指定で確率密度(高さ)が返ります(ここでは後者の指定を必要とするような手続きは登場しません)。
また,求めたいものが下側確率でなく上側や区間のそれであったときには,それぞれの状況にハマる式を組み立てて対応します。
Step 2ある x より小さくなる(※)確率下側確率p
※連続型確率変数がある1点をとる確率=0[cf. 連続確率分布 ―"Wikipedia"]。ここでは「以下」や「以上」といった境界を含む表現と差異はないものと考えます(以下に同じ)。
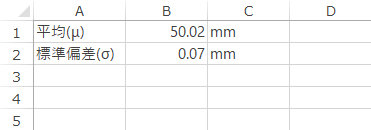
最初に,直径が50.00mmを下回る丸鋼が製造される確率を求めます。x=丸鋼Aの直径50.00mmとしてNORM.DIST関数による計算式を作成すると,下図・下表のようになります。

| B7 | =NORM.DIST(B4, B1, B2, TRUE) |
|---|
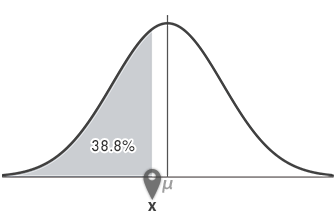
戻り値: 0.388(38.8%)[※少数点第4位で四捨五入。以下に同じ]。これは,下のグラフ[※イメージ。以下に同じ]のグレーの彩色部分の面積です。
Step 3ある x より大きくなる確率上側確率1-p
つづいて,直径が50.05mmを上回る丸鋼が製造される確率を求めます。x=丸鋼Aの直径50.05mmとして,NORM.DIST関数による計算式を作成します。
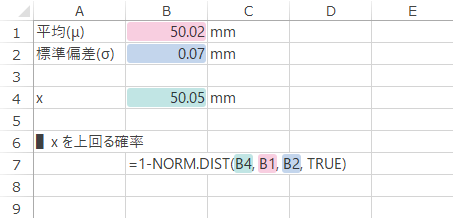
| B7 | =1-NORM.DIST(B4, B1, B2, TRUE) |
|---|
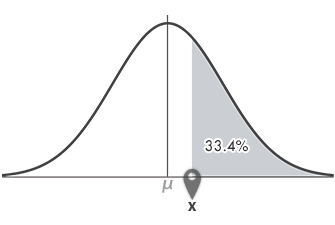
戻り値: 0.334(33.4%)。これは,下のグラフのグレーの彩色部分の面積です。
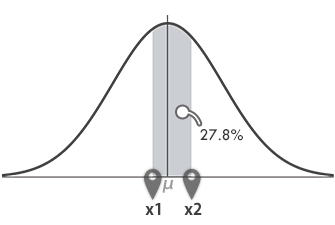
Step 4区間(x1,x2) の値をとる確率px2-px1
Step 2・3の結果を未知と仮定して,直径が50.00mm~50.05mmの丸鋼Aが製造される確率を求めます。x1=丸鋼Aの直径 50.00mm,x2=丸鋼Aの直径50.05mmとしてNORM.DIST関数による計算式を次のように作成します。

| B8 | =NORM.DIST(B5, B1, B2, TRUE)-NORM.DIST(B4, B1, B2, TRUE) |
|---|
戻り値: 0.278(27.8%)。これは,下のグラフのグレーの彩色部分の面積です。
下側確率p または 上側確率1-p から x を求める[パーセント点]
Step 1NORM.INV関数
上と同じシチュエーションを使って,1.とは逆に,下側確率pまたは上側確率1-pと対応する直径x [下側100×pパーセント点 or 上側100×(1-p)パーセント点] を求めていきます。この計算は,ExcelではNORM.INV関数で求めます。このとき,引数は次のとおりです。
- NORM.INV(確率, 平均, 標準偏差) ―"Office"
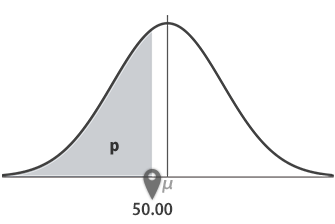
Step 2下側確率p のときの x
最初に,下側確率が0.388(38.8%)のときの直径xを求めます。この場合,p=0.388としてNORM.INV関数による計算式を作成すると,下図・下表のようになります。

| B7 | =NORM.INV(B4, B1, B2) |
|---|
戻り値: 50.00(mm)。これは,下のグラフの横軸・ポインターが指示する点です。
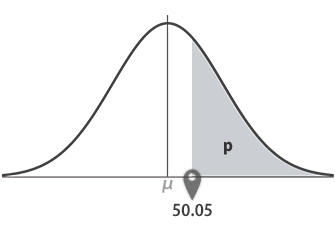
Step 3上側確率1-p のときの x
次に,上側確率が0.334(33.4%)のときの直径xを求めます。1-p=0.334としてNORM.INV関数による計算式を作成すると,下図・下表のようになります。

| B7 | =NORM.INV(1-B4, B1, B2) |
|---|
戻り値: 50.05(mm)。これは,下のグラフの横軸・ポインターが指示する点です。
参考にした書籍
- 菅 民郎(2013)『Excelで学ぶ統計解析入門 Excel2013/2010対応版』オーム社, pp.94-99.
- きたみあきこ(2013)『Excel 関数逆引き辞典パーフェクト 2013/2010/2007/2003対応』翔泳社, pp.648-650.
Next
その他の参照
このサイトの関連How-toです。
- 標準正規分布の確率とパーセント点の計算
- t分布の確率とパーセント点の計算
- χ2分布の確率とパーセント点の計算
- F分布の確率とパーセント点の計算
- 母平均の信頼区間の推定
- 母比率の信頼区間の推定
- 分布曲線のグラフ―確率とパーセント点のビジュアライゼーション
メインサイト「ひとりマーケティングのためのデータ分析」の分布に関連するHow-toです。