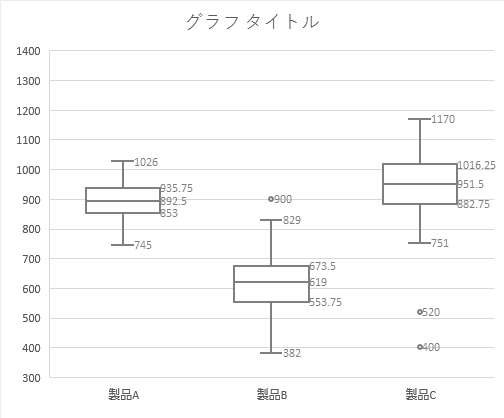
箱ひげ図の作成 with Excel2016,2019新グラフ[Quartile.Inc と Quartile.Exc 関数の違いをふまえて]
イントロダクション
ver.2016から追加された新機能「統計グラフ」のひとつ「箱ひげ図」の作り方です。とはいえ(筆者が)実際に動かしてみたところで,この機能は拍子抜けするくらいに簡単に エクセルという制約の上でもよくできたグラフをつくり上げてしまうシロモノだと感じました(念のため,肯定的な意味です)。
おそらく「箱ひげ図って何?」を知らなくても作れてしまう程度の簡単さと言っていいと思います。箱ひげ図は本来ヒストグラムと同じく,ものすごくディープなしくみをもつものだと個人的には思いますので,少し大げさに言えば,アウトラインを無視したままアウトプットに到達できてしまいます。それはリスクにもなりえますので,ここでは手順そのものは従とすることにして,Excel版に照らした“箱ひげ図のしくみ・構造”的な駄文を綴っていきたいと思います。
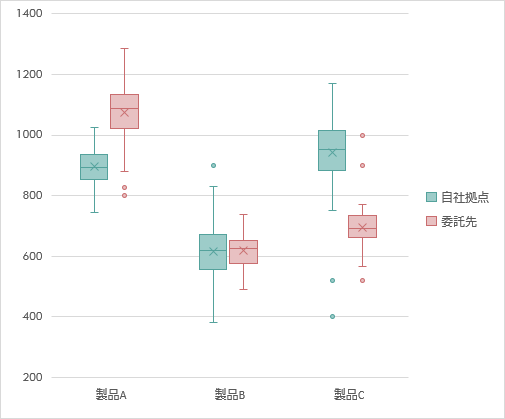
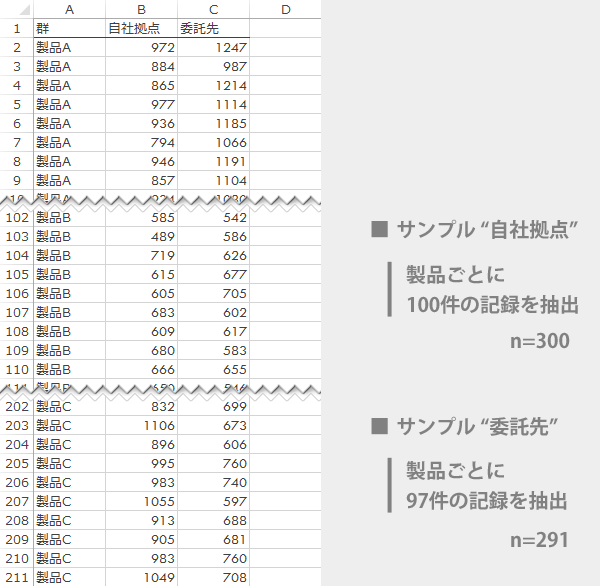
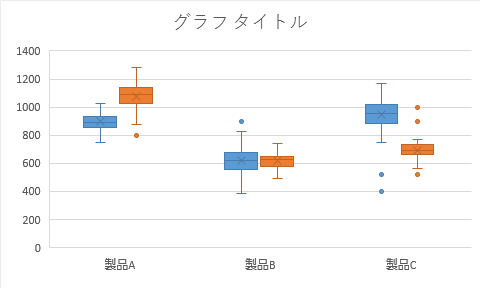
テストデータは以下のものを使います。3群からなる2つのサンプルです(新グラフは,複数の群・サンプルでも特段の加工なしに処理できるようです)。
架空のメーカーX社の製品A,B,Cに関する問い合わせ窓口業務を,同社は2拠点体制(自社拠点,委託先)で運営しています。両拠点での問い合わせ案件ごとに要した対応時間(秒)の記録を,各製品ごとに,自社拠点では100件ずつ,委託先では97件ずつ無作為に抽出したのが下表です(n=300, n=291)。
DL
作成にあたり参考にしたWebページ
- [Web]Visualize statistics with Histogram, Pareto and Box and Whisker charts ―"Office Blogs" url:https://blogs.office.com/2015/08/18/visualize-statistics-with-histogram-pareto-and-box-and-whisker-charts/ (2015.10 閲覧; リンク切れ; 現リンク)
- [Web]Why Excel has Multiple Quartile Functions and How to Replicate the Quartiles from R and Other Statistical Packages ―"Bacon Bits" url:http://datapigtechnologies.com/blog/index.php/why-excel-has-multiple-quartile-functions-and-how-to-replicate-the-quartiles-from-r-and-other-statistical-packages/ (2015.10 閲覧; リンク切れ)
- [Web]離散分布の分位数, 箱ひげ図 ―"五捨五超入と四分位数と放射線のサイト"(2015.10 閲覧)
- [Web]Create a box and whisker chart ―"Office"(2015.10 閲覧)
箱ひげ図の作成 with Excel2016,2019 新グラフ
手順
Step 1新グラフ「箱ひげ図」
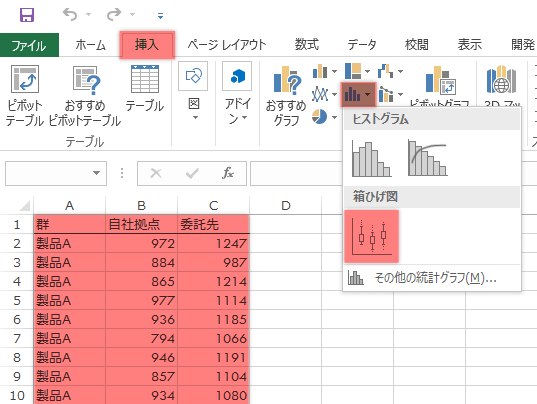
データ範囲を見出しも含めて選択し,挿入タブ「グラフ」グループの統計グラフの挿入ボタンをクリックします。
そのまま「箱ひげ図」グループから箱ひげ図ボタンを選択します。
Step 2グラフ|箱ひげ図を構成する諸要素(1)
次のようなグラフが出力されます。
ここではおこないませんが,サンプルが複数の場合通常のグラフと同様凡例もきちんと挿入できます(最初に掲示したイメージ図のような)。
以下しばらくグラフの構成要素に関して触れます。
例示のため,グラフのなかから1つの系列をクローズアップしたとき次の要素は「箱」
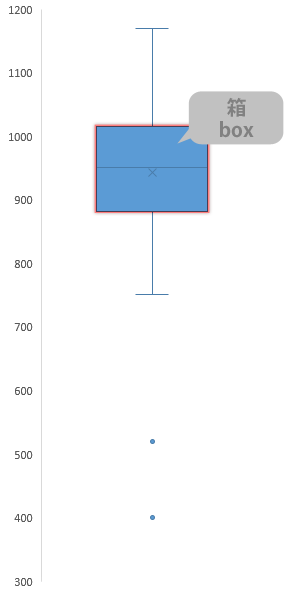
次の要素は「ひげ」と呼びます。
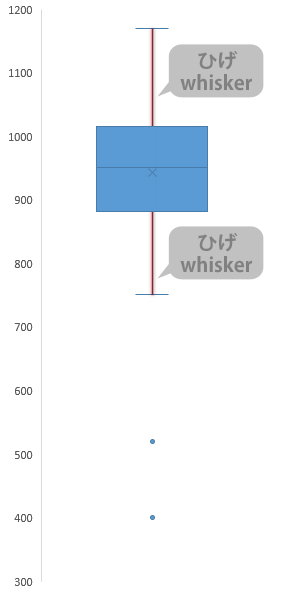
また,元にしたデータによっては「箱・ひげ」の部分からいくらか離れたところに1つ,または複数の「外れ値」と呼ばれるマーカーがあらわれることがあります。
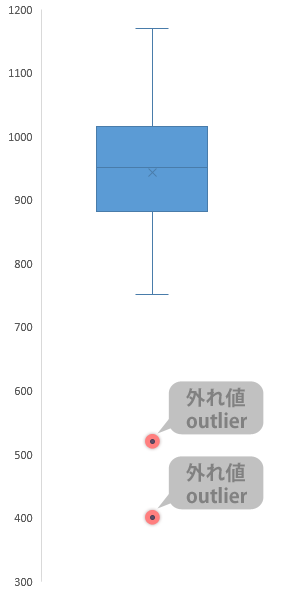
Step 3グラフ|箱ひげ図を構成する諸要素(2)
「箱」の構成要素にも役割があって,これらは下の線から順に「第1四分位数」「第2四分位数(中央値)」「第3四分位数」を意味します。
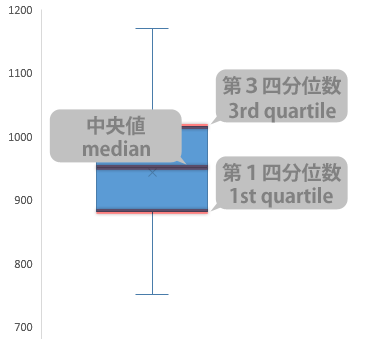
同様に,「ひげ」の突端にも役割があり,通常,これらは下の線から順に「最小値」「最大値」を意味しますが…
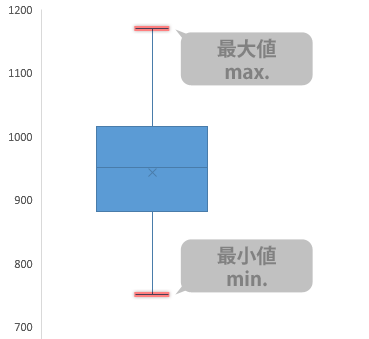
上下いずれか,あるいはその両方向に「外れ値」が表示されている場合は,(外れ値が存在するサイドでのみ)とりあえずそれらをないものとして考えたとして,下から順に,元のデータに実際に登場している最も小さな値と,最も大きな値とを意味します。
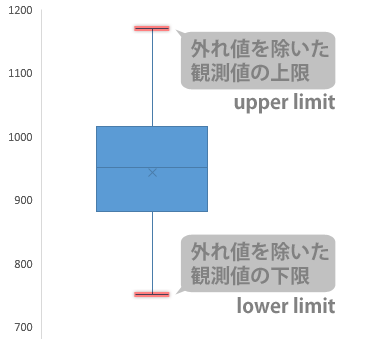
いずれの場合にしろ,最小値~箱の下側の線(第1四分位数),箱の下側の線~箱の真ん中の線(中央値),箱の真ん中の線~箱の上側の線(第3四分位数),箱の上側の線~最大値 の各区間は,全体のうち,およそ1/4の観測値を含むことになります。
では「外れ値」になるデータと「箱」または「ひげ」を構成するデータとでは何がちがうのかといえば
箱の下側の線(第1四分位数)と上側の線(第3四分位数)をそれぞれスタート地点として,前者は線から下,後者は線から上方向に,箱の高さの1.5倍の長さのものさしを置いて判断します。
このものさしでも届かないところにあるデータを,すべて機械的に“外れ値”とします(この新グラフではできませんが,もちろんこれ以外の判断の方法もあります。ただし,この新グラフが採用している方法はおそらくもっともスタンダードと言える方法です)。
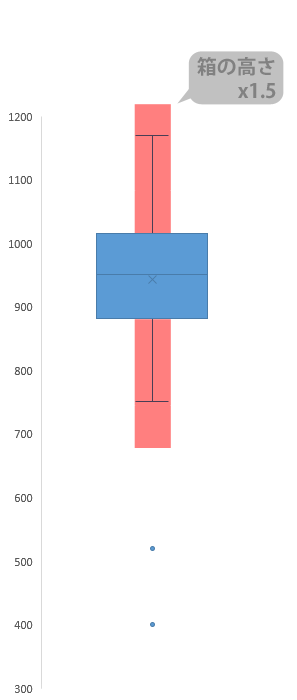
箱の中のマーカー(×印)は「平均」を意味します。エクセルではデフォルトで表示される設定です。
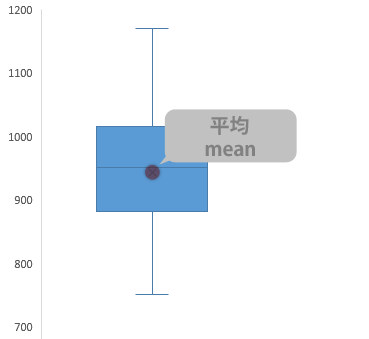
設定|外れ値・平均値
Step 4グラフ|書式設定
ここからは設定可能な項目を見ていきます。設定はすべて作業ウインドウでおこないます。と,いうことで
グラフをアクティブにし,書式タブ「現在の選択範囲」グループの選択対象の書式設定ボタンをクリックします。
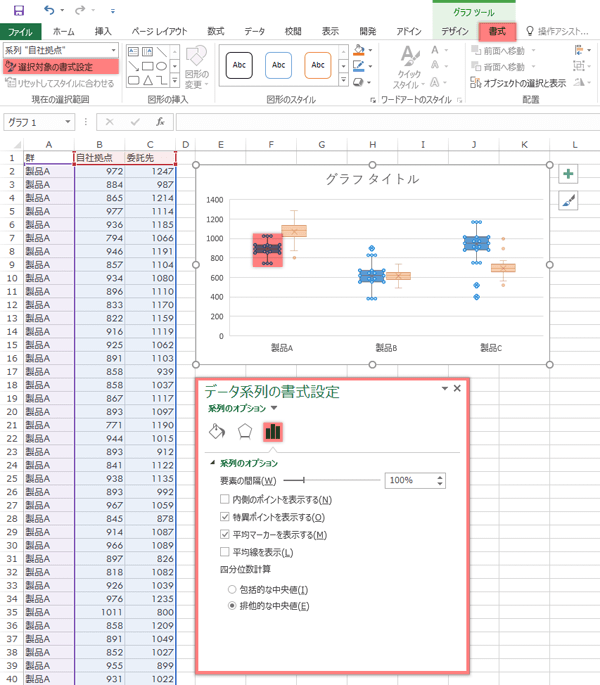
Step 5グラフ|「特異ポイント」「平均マーカー」
はじめに,デフォルトで「特異ポイントを表示する」「平均マーカーを表示する」にチェックが入っていることと思います。
これらは順に,先に見た 外れ値を表示するかしないか,平均マーカーを表示するかしないか,を制御します。これらのチェックを外す必要に迫られる機会は,ごく少ないかもしれません。
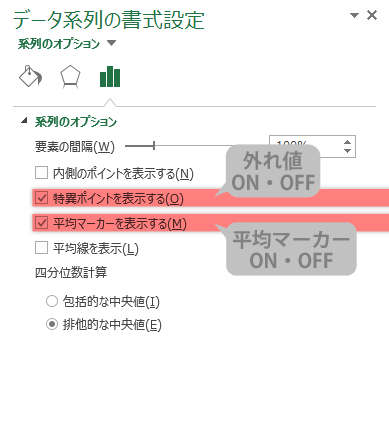
設定|四分位数
Step 6グラフ|「包括的な中央値」「排他的な中央値」
つづいて「四分位数計算」カテゴリを見ていきます。
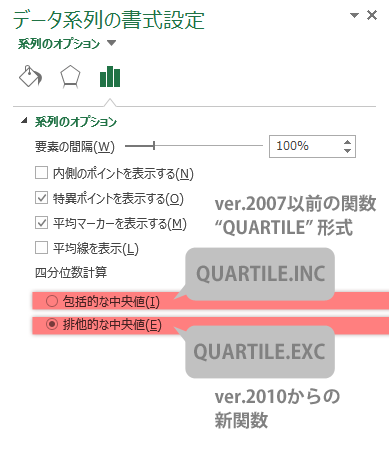
「包括的な中央値」「排他的な中央値」の排他的な選択肢があり,デフォルトでは「排他的な」の方になっています。先の外れ値の判定のしかたと同じく,この四分位の計算にもいろいろな方法(アルゴリズム)があって,エクセルではこの2つを選択できるということです。
これらはもともと組み込みの関数によって求めることができ,「包括的な中央値」は“quartile.inc”(quartile に同じ)によるアウトプットと,「排他的な」の方は“quartile.exc”によるアウトプットと同様のものです。
ならば,これらはどう異なるのか? という点が次に気になるところです。少なくとも筆者には「包括的な」「排他的な」という字面だけで差異を理解しろと言われても不可能です。ちなみに相当関数の公式ヘルプに頼ってみると
0~1の間 (0および1を含む) の百分率の値に基づいて,データの配列の四分位数を返します
―Quartile.Inc0~1の間(0および1を除く) の百分率の値に基づいて,データの配列の四分位数を返します
―Quartile.Exc
とあり「ぐぬぬ…」な感じでした。筆者ならこれで察しろと言われるのはあまりに突き放された孤独を感じるので,ここでは筆者なりの単純な理解を別のアプローチから以下にまとめておきたいと思います。
例示のため,小さな順から並んだ 次の5つの値をつかって「包括的な」「排他的な」のちがいを考えます(n=5)。

まず,中央値は左から何番目の値第1四分位数は左から何番目の値という点を考えたいと思います。
具体的には,次の2つの考え方を用意します。最初に,いちばん左の値から1番2番と数えていく方法,次に,同じくいちばん左の値から0番1番 と数えていく方法を想起します。便宜的に,ここでは前者をn+1法, 後者をn-1法と呼ぶものとします。上下が逆になりますが,下図では,n+1法の採番は下,n-1法の採番は上でおこないました。
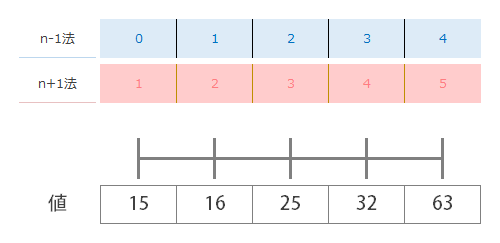
ヘルプにいう 百分率の値に基づいて
第1四分位, 第2四分位, 第3四分位を求めます。第1四分位は下から1/4つまり0.25(25%)の点,第2四分位は2/4つまり0.5(50%)の点,第3四分位は3/4つまり0.75(75%)の点なので,これらをn-1,n+1に乗じます。具体的には,下表のような式ができ
| 第1四分位 | 第2四分位 | 第3四分位 | |
| n-1法 | (5-1)*0.25 | (5-1)*0.5 | (5-1)*0.75 |
| n+1法 | (5+1)*0.25 | (5+1)*0.5 | (5+1)*0.75 |
これらを逐次計算して,次のような値を導くことができます。
| 第1四分位 | 第2四分位 | 第3四分位 | |
| n-1法 | 1 | 2 | 3 |
| n+1法 | 1.5 | 3 | 4.5 |
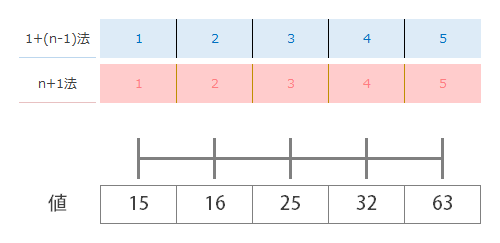
上の表は,それぞれの方法の採番をものさしの目盛の数字に見立てたとき,第1四分位,第2四分位,第3四分位がそれぞれものさしの目盛でいうどの位置にあるのかを教えてくれます。
それぞれの方法に対応する目盛を間違えないように注意しながら,上の表で求めた値を目盛の上にプロットしていった結果,下の図のようになりました。
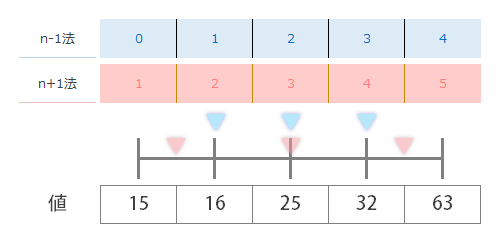
n-1法(青)の方のマーカーの位置は“4等分”という意味ではまぁ…腑に落ちるわけですが,n+1法(赤)の結果は何だか等分とは呼べないような…そんなもやもやが残ります。そこで,つづいては実際の値のブロックの方(図のいちばん下)で確かめてみたいと思います。
ということで,ここでもあらたにものさしを用意します。いちばん左の値のブロックから,それぞれの方法が示した最初のマーカーまでの長さを得たものさしを作って,これをブロックの上に置いてみます(ものさし×1)。
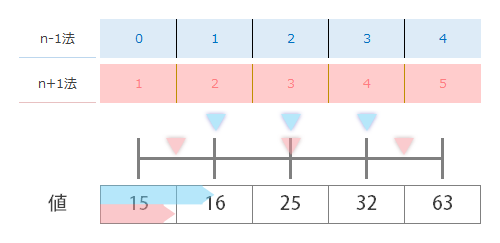
つづいて,2つ目のものさしを右隣にならべます(ものさし×2)。
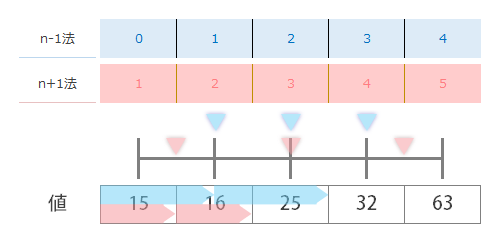
今度はいちばん右の値のブロックから,上と同様にならべてみます(ものさし×3)。
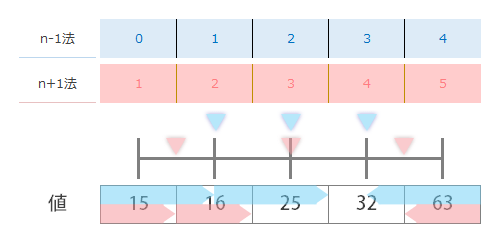
こちらもつづいて,4つ目のものさしを左隣にならべます(ものさし×4)。
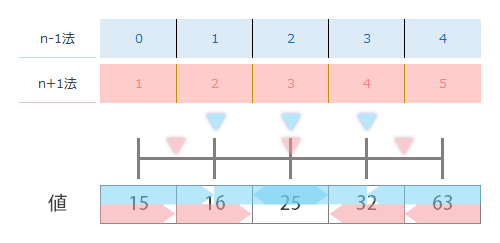
ここであらためて最初にあげた設定画面を再掲して上の図の結果と照らし合わせてみると…

中央値を「包括」「排他」の意味がおぼろげに察せられてきます。要するに「包括的な」の方は計算において中央値を含み,「排他的な」の方は含めません。第2四分位(中央)はどちらの方法でも同じになりますが,第1・3四分位は両方法で異なってきます。
さて,ここでn-1法,n+1法ともに目盛の先にある値を読んでみます。まずn-1法(青)からですが
マーカーを打った場所が目盛とドンピシャ(=先に求めた値が整数)なので,下のブロックの数字を読むのに苦労はありません。左のマーカーから順に,16, 25, 32を指しているのがわかります。すなわち,それらは順に 第1四分位, 第2四分位, 第3四分位の内容(四分位数)となります。
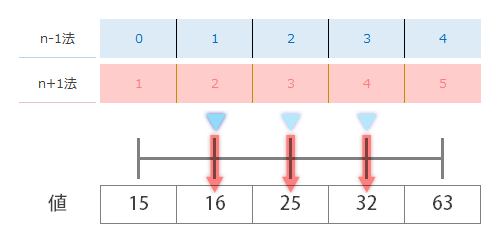
転じて,ここでn+1法(赤)も同じようにしてみましたが…中央値以外は目盛ドンピシャじゃないので値を読むのが少しめんどうになります。ええと…自然な感覚的には…これは 第1四分位数は値15,16の真ん中なので15.5,第3四分位数は値32,63の真ん中なので47.5と読めばいいような気もします。
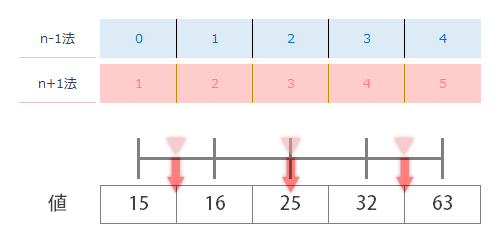
ここまでの過程で見たように,四分位数を測るのに毎度毎度目盛を描いてるわけにもいきませんが,実のところ,今おこなった方法は分位数を求めるにあたってのたくさんの方法のなかのひとつとなります。「包括的な」「排他的な」に相当するQuartile.IncおよびQuartile.Exc関数はこれとは少し異なる「線形補間」と呼ばれる方法で分位数を解決します。
ただ,線形補間を用いるにあたっては,ここまでにおこなってきた採番のしかたを少し変えてやった方がおそらくはかどると思います。具体的には,n-1法の採番のしかたを変えて,1+(n-1)法としてやります。
何がしたいのかと言えば,n-1に1を加えて,n+1法の採番のしかたとまったく同じにしてしまいたいのです(目盛が揃う)。
したがって,分位数を旧n-1法についてのみ再度計算しなおします。
| 第1四分位 | 第2四分位 | 第3四分位 | |
| 1+(n-1)法 | 1+(5-1)*0.25 | 1+(5-1)*0.5 | 1+(5-1)*0.75 |
結果↓
| 第1四分位 | 第2四分位 | 第3四分位 | |
| 1+(n-1)法 | 2 | 3 | 4 |
もちろん目盛の位置関係は以前と変わるものではありません。

ではこの分位と値の一覧から,下式を使って線形補間により分位数を求めてみます。式の中に,ユーザーによってはあまり見かけることのないかもしれない床関数や天井関数といったややこしそうな記号が登場します。これはExcelでも専用の関数がある(順にFloor系,Celling系)ので,そう悩むこともなく式はつくれるはずです。
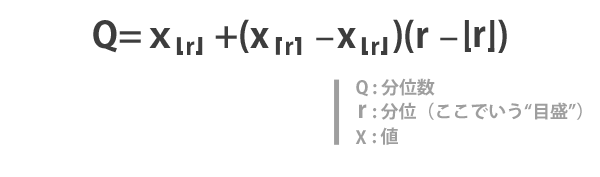
シート上に先ほどの目盛と値とを対応させて表をつくり
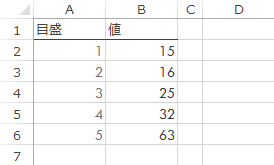
その右側へすでに求めてある各分位を入力します。
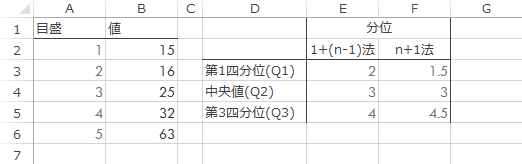
さらに右方の列に表組みを作成し,彩色したセルに先の式をもとに作成したExcelでの式※を入力してこれをコピーすると
※式の中にSmall関数がいっぱい並ぶと,前言を否定するようでなんなんですが,やっぱりややこしそうに見え(ry
| G3 | =SMALL($B$2:$B$6, FLOOR.MATH(E3))+(SMALL($B$2:$B$6, CEILING.MATH(E3))-SMALL($B$2:$B$6, FLOOR.MATH(E3)))*(E3-FLOOR.MATH(E3)) |
|---|
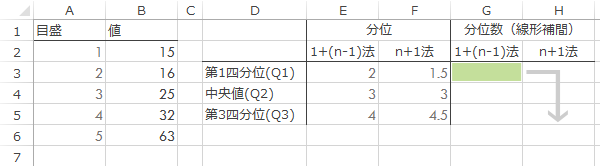
下のような値がでてきます。このとき
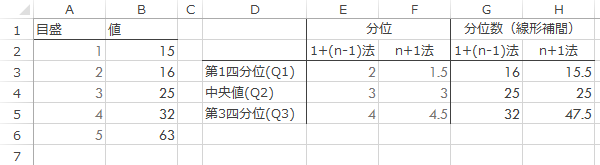
左側の値がQuartile.Incと,右側の値がQuartile.Excの戻り値と等しくなります。

Quartile.Inc,Quartile.Excのいずれにしろ,第1四分位数から第3四分位数の幅(Q3-Q1: 四分位範囲,IQR)が箱の高さになり,
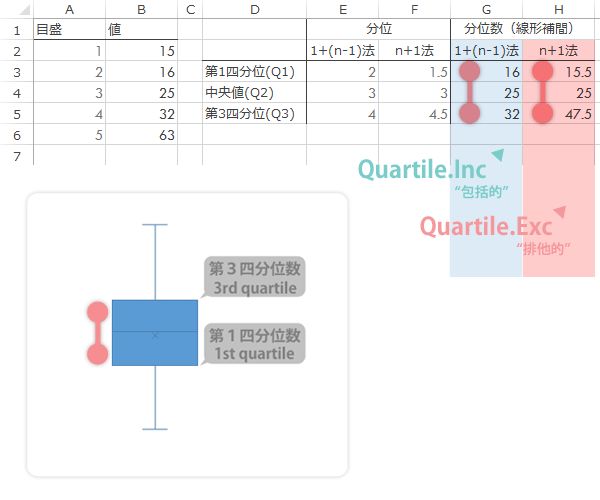
先に見たとおり,中央値を計算に含めない分,Quartile.Excによる戻り値の方が箱の高さは高くなります。

ここで,外れ値が箱の高さの1.5倍のものさしを基準にして決められた点をふりかえると(再掲)…

Quartile.IncとQuartile.Excとの比較では,リクツ的には,前者は(元データの性質により程度はありますが)外れ値が出やすく,後者は外れ値が出にくいといった性質をもつことがわかります。
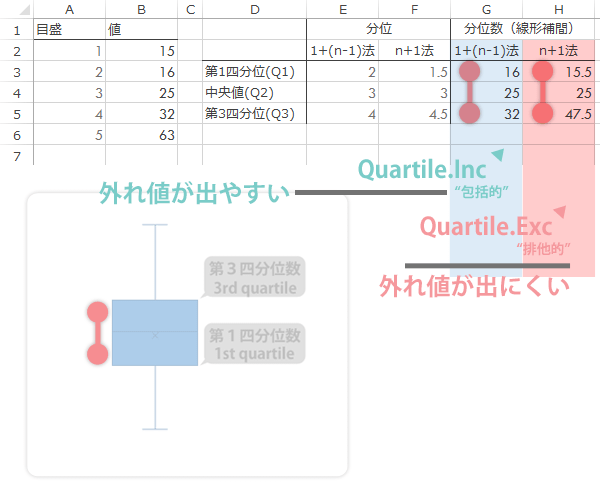
その意味では,外れ値の扱いをよりシビアにするかどうかでQuartile.IncとQuartile.Excの選択, 箱ひげ図の設定でいえば「包括的」と「排他的」の選択を判断すればいいかと思います。
またこちらの解説(「図の出所」に掲示のリンク先; リンク切れ)によると,Quartile.Exc方式は,近時Excel以外の主要な統計パッケージ間でも広く利用可能なアルゴリズムとなっているようです。エクセル2016の新グラフ「箱ひげ図」が「排他的」を四分位数計算のデフォルトのアルゴリズムとしてきたのも,こうした趨勢を斟酌してのことかもしれません。
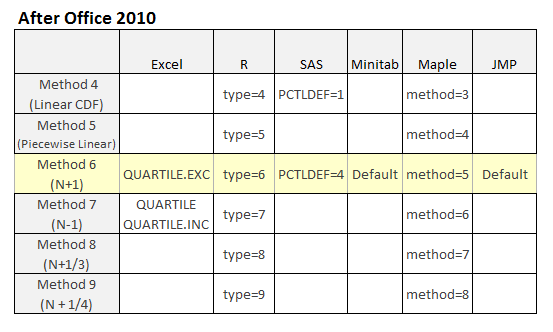
[図の出所]Why Excel has Multiple Quartile Functions and How to Replicate the Quartiles from R and Other Statistical Packages -"Bacon Bits"(http://datapigtechnologies.com/blog/index.php/why-excel-has-multiple-quartile-functions-and-how-to-replicate-the-quartiles-from-r-and-other-statistical-packages/ ;リンク切れ)
もっとも,現実には観測条件の継続性といった点にはとりわけ慎重であるべきでしょう。後方互換性のあるQuartile関数によるひな形を使って過去継続的に箱ひげ図を記録してきた場合など,新グラフの「排他的」のラジオボタンを塗りつぶす作業が1クリックで済むほど軽いものとはならない場合もあります。
設定|データポイント
Step 7グラフ|「内側のポイントを表示する」
以下,残りの設定箇所の話です。
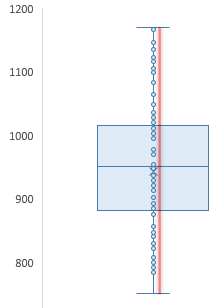
「内側のポイントを表示する」のチェックを入れると,外れ値以外の元データを別途マーカーで表示します。
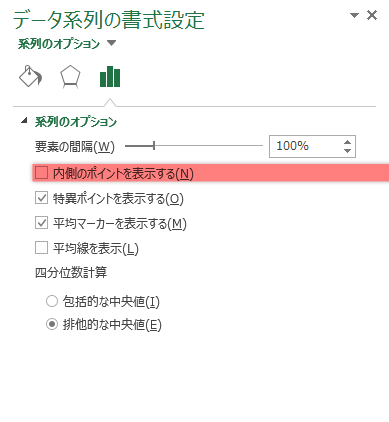
具体的には,次のように外れ値と同じ書式で描画されます。これによって,ある意味で箱ひげ図の弱点たる“分布の細かなクセ”を知ることができない点に関して若干は補うことができます。
これを補うことの意義については,こちらの論文「データ分析における「箱ひげ図」の誤解-高校教科書における多数の誤り-」に多くの示唆があります。
ただ,このあたらしいグラフにかかわる注意がいるかもしれない点を1つだけあげておくと,これらデータポイントは何らかのアルゴリズムで端折られるやもしれません(検証できていませんが,上のグラフを見ても,マーカーが100個近くあるようには見えません。もちろん,座標が重なったものもあるので軽々と断定はできませんし,サンプルサイズの大小も考える必要があります)。このへんは欲を言えば,ビースウォームやドットヒストグラムなど機能で補完できたらいいなと強く思わせるところです。
設定|平均線
Step 8グラフ|「平均線を表示」
「平均線を表示」です。
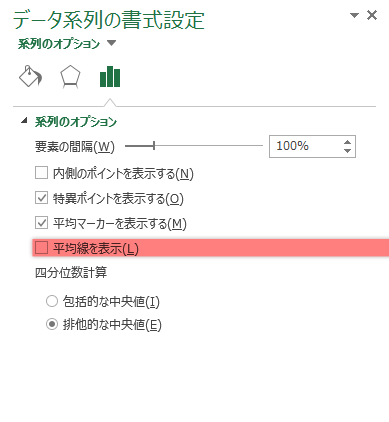
これは下のように指定した系列の平均マーカーをx軸方向に折れ線グラフのようにして結びます。変数を時系列で観察していくようなときには,役に立つかもしれません。
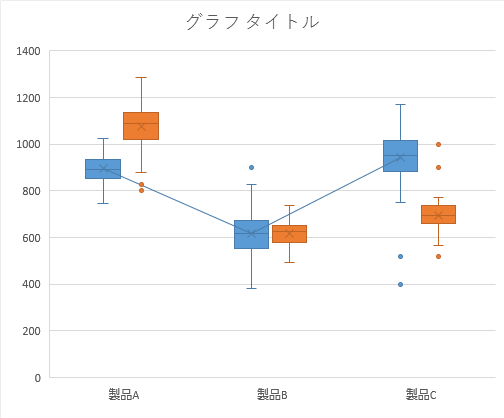
その他要素|データラベル
Step 9グラフ|「データラベル」
最後にこれは固有機能ではないですが,きちんとデータラベルも挿入できます。任意のラベルを個別に選んで削除することも可能です。またラベル位置も他のグラフと同様4方向を排他的に選択して設置することができますが,筆者の試した限りでは位置に関する微調整が効かない点で惜しいかな制約を抱えるようです。